| Issue |
Math. Model. Nat. Phenom.
Volume 2, Number 1, 2007
Epidemiology
|
|
|---|---|---|
| Page(s) | 84 - 112 | |
| DOI | https://doi.org/10.1051/mmnp:2008012 | |
| Published online | 15 June 2008 | |
An Intracellular Delay-Differential Equation Model of the HIV Infection and Immune Control
1
Department of Mathematics, Faculty of Science, Chiangmai University
Chiangmai, 50200 Thailand
2
Department of Mathematics, Faculty of Science, Mahidol University
Bangkok, 10400 Thailand
3
Department of Mathematics, Syracuse University, Syracuse, NY 12344, USA
Corresponding author: rujira@chiangmai.ac.th
Previous work has shown that intracellular delay needs to be taken into account to
accurately determine the half-life of free virus from drug perturbation experiments [1]. The delay
also effects the estimated value for the infected T-cell loss rate when we assume that the drug is
not completely effective [19]. Models of virus infection that include intracellular delay are more
accurate representations of the biological data.
We analyze a non-linear model of the human immunodeficiency virus (HIV) infection that
considers the interaction between a replicating virus, CD4+ T-cell and the cytotoxic-lymphocytes
(CTL).We then investigate the intracellular delay effect on the stability of the endemically infected
steady state. Criteria are given to ensure that the infected steady state is asymptotically stable for
all delays. Model analysis also allows the prediction of a critical delay 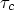 below which the effector
CTL can play a significant role in the immune control mechanism even when the basic reproduction
number is high.
below which the effector
CTL can play a significant role in the immune control mechanism even when the basic reproduction
number is high.
Mathematics Subject Classification: 34A34 / 37N25 / 92B05
Key words: delay system / CD4+T-cell / the HIV infection and immune control
© EDP Sciences, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


