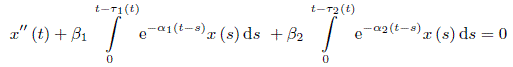Stabilization by delay distributed feedback control

Department of Mathematics, Ariel University, Ariel, Israel

^* e-mails: adom@ariel.ac.il, irinav@ariel.ac.il

Received: 2 October 2017
Accepted: 2 October 2017

Abstract

In this paper, a new approach to stability of integro-differential equations $$x^{\prime \prime }\left(t\right)+{\beta }_1\underset{t-{\tau }_1\left(t\right)}{\overset{t}{\int }}{e}^{-{\alpha }_1\left(t-s\right)}x\left(s\right)ds+{\beta }_2\underset{t-{\tau }_2\left(t\right)}{\overset{t}{\int }}{e}^{-{\alpha }_2\left(t-s\right)}x\left(s\right)ds=0$$

and $$x^{\prime \prime }\left(t\right)+{\beta }_1\underset{0}{\overset{t-{\tau }_1\left(t\right)}{\int }}{e}^{-{\alpha }_1\left(t-s\right)}x\left(s\right)ds+{\beta }_2\underset{0}{\overset{t-{\tau }_2\left(t\right)}{\int }}{e}^{-{\alpha }_2\left(t-s\right)}x\left(s\right)ds=0$$

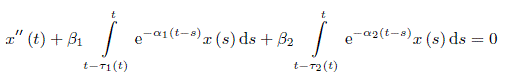
is proposed. Under corresponding conditions on the coefficients α₁, α₂, β₁ and β₂ the first equation is exponentially stable if the delays τ₁ (t) and τ₂ (t) are large enough and the second equation is exponentially stable if these delays are small enough. On the basis of these results, assertions on stabilization by distributed input control are proven. It should be stressed that stabilization of this sort, according to common belief, requires a damping term in the second order differential equation. Results obtained in this paper demonstrate that this is not the case.