| Issue |
Math. Model. Nat. Phenom.
Volume 8, Number 1, 2013
Harmonic analysis
|
|
|---|---|---|
| Page(s) | 193 - 199 | |
| DOI | https://doi.org/10.1051/mmnp/20138114 | |
| Published online | 28 January 2013 | |
Heat Transfer in a Medium in Which Many Small Particles Are Embedded
Department of Mathematics Kansas State
University, Manhattan, KS
66506-2602,
USA
The heat equation is considered in the complex system consisting of many small bodies
(particles) embedded in a given material. On the surfaces of the small bodies a
Newton-type boundary condition is imposed. An equation for the limiting field is derived
when the characteristic size a of the small bodies tends to zero, their
total number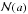 
tends to infinity at a suitable rate, and the distance
d = d(a) between neighboring small
bodies tends to zero a < < d. No periodicity is
assumed about the distribution of the small bodies.
Mathematics Subject Classification: 35K20 / 35J15 / 80M40 / 80A20
Key words: heat transfer / many-body problem
Corresponding author. E-mail: ramm@math.ksu.edu
© EDP Sciences, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.