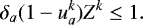| Issue |
Math. Model. Nat. Phenom.
Volume 15, 2020
Coronavirus: Scientific insights and societal aspects
|
|
|---|---|---|
| Article Number | 48 | |
| Number of page(s) | 21 | |
| DOI | https://doi.org/10.1051/mmnp/2020035 | |
| Published online | 14 October 2020 | |
Optimal control techniques based on infection age for the study of the COVID-19 epidemic*
1
INRIA-Saclay and Centre de Mathématiques Appliquées, Ecole Polytechnique,
91128
Palaiseau, France.
2
CIFASIS-CONICET-UNR, Ocampo y Esmeralda, S2000EZP,
Rosario, Argentina.
** Corresponding authors: frederic.bonnans@inria.fr; gianatti@cifasis-conicet.gov.ar
Received:
18
May
2020
Accepted:
3
September
2020
We propose a model for the COVID-19 epidemic where the population is partitioned into classes corresponding to ages (that remain constant during the epidemic). The main feature is to take into account the infection age of the infected population. This allows to better simulate the infection propagation that crucially depend on the infection age. We discuss how to estimate the coefficients from data available in the future, and introduce a confinement variable as control. The cost function is a compromise between a confinement term, the hospitalization peak and the death toll. Our numerical experiments allow to evaluate the interest of confinement varying with age classes.
Mathematics Subject Classification: 49M25 / 92D25 / 92D30 / 35Q93
Key words: COVID-19 / epidemic modeling / confinement / age-structured systems / optimal control
© The authors. Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The COVID-19 epidemic appears for the first time in Wuhan, China at the end of 2019. It quickly spread throughout the world, and on March 12, 2020 it was declared a pandemic by the World Health Organization (WHO). So far there are no vaccines and it is not clear if there is any effective treatment to combat it. That is why the governments of the different countries began to implement containment measures in the population, trying to control the disease. Since these actions have a great impact on the daily life of the population, one of the big questions now is knowing how long to carry out these measures.
The recent COVID-19 epidemic has already been modelized in e.g. [8–10]. These papers use variants and extensions of the SIR (Susceptible-Infected-Recovered) model based on ODEs (ordinary differential equations). SIR is the standard approach for the modelization of epidemics and takes its origin in [7]. Of course it is difficult to model confinement. The simplest way is to assume that it boils down to a multiplicative factor coefficient with value in [0, 1] in the formula for new infections. That is, the dynamics in the SIR setting would be
 (1.1)
(1.1)
with δ > 0 infection coefficient, η > 0 death rate, and μ > 0 recovery rate. Observe that, here as in the sequel, our models do not take into account birth, as well as death for other reasons than the epidemic itself. We recover the classical SIR dynamics in the case of an uncontrolled system, i.e., when u(t) = 0 for all t. Total confinement is out of reach and therefore we may assume that we have the control constraint u(t) ≤ uM, with uM ∈ (0, 1). Of course it is not easy to specify a confinement cost, but we might take
 (1.2)
(1.2)
with pu ≥ 0 penalty factor, and for example φ(s) = s (as we did in our numerical tests) or φ quadratic.
Our proposal is to distinguish, among infected people, those who are hospitalized and those who are not, and to take into account the limited duration of the infection. The latter can be achieved by associating with the infected population an “infection age" variable. That also allows us to differentiate between the incubation and infectious phases of the disease. Furthermore, since the severity of this COVID-19 seems to depend on the age of the infected population, it may be useful to take into account the population age, in addition to the infection age. The cost function will minimize a combination of confinement cost, value of hospitalization peak, and death toll.
Concerning the optimal control of age-structured population, see [4] (without diffusion), and [1] (with diffusion). The optimal control of age models with state constraints is discussed in [3]. About optimal control application to epidemiological models, see e.g. [11]. About the related question of models involving delays, see e.g. [13]. On optimal control approaches for COVID-19, see [5]. During the revision process, we noticed the appearance of [12] that also propose an optimal control model with infection age. The main difference with respect to our model is that we consider the peak value in the objective function, which leads to a problem with state constraints. Let us also mention a mean field game approach to the COVID-19 epidemic [6].
The paper is organized as follows. In Section 2, we present a continuous time (and infection age) optimal control problem. The corresponding discrete time problem is discussed in Section 3. The data analysis (how to estimate thecoefficients of the problem) as well as the initial conditions are the subject of Section 4. Finally, in Section 5, we discuss various numerical results. The paper ends with a conclusion giving a perspective of possible extensions.
Our open access code, based on the optimal control toolbox Bocop http://www.bocop.org, can be downloaded from http://www.cmap.polytechnique.fr/~bonnans/covid-19/covid-19.html or https://www.fceia.unr.edu.ar/~justina/covid-19/.
2 Continuous time optimal control problem
2.1 An infection age structured model
We have two kinds of patients, the exposed ones, who are asymptomatic or with mild symptoms, and those who need hospitalization. Let z(t, a, b) (resp. h(t, a, b)) denote the number of exposed (resp. hospitalized) patients of age a ∈ [0, A] at time t, that have been infected for duration b ∈ [0, B]. Here A and B are positive constants. Let y(t, a) (resp. ȳ (t, a)) denote the number of non-immunized (resp. immunized) people of age a at time t. Since in practice the age variable a does not significantly vary during the epidemic, we assume that individuals keep the same age over time. The control variable u(t, a) ∈ [0, 1] is the confinement policy (no confinement if u(t, a) = 0, total confinement if u(t, a) = 1). We considerthe following dynamics
![\begin{equation*}\left\{\begin{array}{l} \dot{y}(t,a)=-\delta(a)(1-u(t,a))Z(t)y(t,a)\\[6pt] y(0,a)=y_0(a),\\[6pt] (z_t+z_b)(t,a,b)=-\nu(a,b)z(t,a,b)\\[6pt] z(0,a,b)=z_0(a,b)>0,\;\;\;\;z(t,a,0)=\delta(a)(1-u(t,a))Z(t)y(t,a)\\[6pt] (h_t+h_b)(t,a,b)=\nu(a,b)z(t,a,b)-\left(\eta(a,b) + \gamma(a,b) E(t)\right) h(t,a,b)\\[6pt] h(0,a,b)=h_0(a,b)\geq 0, \;\;\;\;h(t,a,0)=0\\[6pt] \dot{{\bar{y}}}(t,a)=z(t,a,B)+h(t,a,B)\\[6pt] {\bar{y}}(0,a)=0.\\[6pt] \end{array} \right. \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq3.png) (2.1)
(2.1)
Here, δ(a) ≥ 0 is the “transmission coefficient”, Z(t) is the “global transmission factor", modelled as
 (2.2)
(2.2)
with e(a, b) ≥ 0 “transmission factor" (we assume that hospitalized patients do not contribute to the transmission of the disease). Also, ν(a, b) ≥ 0 is the hospitalization coefficient, and E(t) ∈ [0, 1] is the hospital saturation estimate, given by
 (2.3)
(2.3)
where C > 0 is the nominal capacity. We assume that only hospitalized patients die, with death rate
 (2.4)
(2.4)
where η(a, b) ≥ 0 is the minimal death rate and γ(a, b) sensitivity of the death rate w.r.t. the hospital saturation estimate.
Remark 2.1.
In our numerical tests we will assume that there exists an incubation phase [0, n0) during which transmission and hospitalization do not occur. Additionally, in the infectious phase for which b ∈ [n0, B], we assume that e(a, b) = 1 and that ν(a, b), η(a, b) and γ(a, b) have constant values denoted by  ,
,
 and
and
 resp. Then, the coefficients take the form:
resp. Then, the coefficients take the form:
![\begin{equation*} e(a,b)= \mathbb{1}_{[n_0,B]}(b), \;\;\; \nu(a,b)=\mathbb{1}_{[n_0,B]}(b){\bar{\nu}}(a), \;\;\; \eta(a,b)=\mathbb{1}_{[n_0,B]}(b){\bar{\eta}}(a),\;\;\text{and}\;\; \gamma(a,b)=\mathbb{1}_{[n_0,B]}(b){\bar{\gamma}}(a). \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq10.png) (2.5)
(2.5)
Consequently, h(t, a, b) = 0 whenever b ∈ [0, n0] and
 (2.6)
(2.6)
So, in this case, the model has four parameters for each value of a: δ(a),  ,
,  and
and  .
.
2.2 Optimal control problem
We next introduce the cost function to be minimized. Given the horizon T, the death toll for age a is equal to the difference between the initial and final population for this age:
![\begin{equation*} \begin{array}{ll} D(a) :=& y(0,a)+{\bar{y}}(0,a) +\int_0^Bz(0,a,b)+h(0,a,b)\textrm{d} b\\[6pt] \;&- \left( y(T,a)+{\bar{y}}(T,a)+\int_0^B\left(z(T,a,b)+h(T,a,b)\right)\textrm{d} b\right). \end{array} \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq15.png) (2.7)
(2.7)
The total death toll is  Denote by
Denote by
 (2.8)
(2.8)
the weighted confinement cost, with weights ce(a) ≥ 0. The cost to be minimized is a combination of several costs. Its expression is
 (2.9)
(2.9)
where the penalty coefficients pM, pu and pD are nonnegative. Here M is an additional variable, called the peak value, subject to
![\begin{equation*} H(t)\leq M, \quad\forall t\in[0,T]. \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq19.png) (2.10)
(2.10)
Indeed, if pM is nonzero, theoptimal M will be the minimal hospital capacity needed to take care in an optimal way of all patients, which justifies the peak value terminology.The ability to minimize this amount has been recognized of paramount importance.
The second term in the cost function involves the weighted confinement effort. The associated economic cost is difficult to evaluate; this question being out of the scope of the present paper, we simply take it linear with somewhat arbitrary weights, having in mind the obvious fact that the confinement of retired people has a smaller economic impact than for the rest of the population, although psychological aspects should also be taken into account.
Finally, remember that the death rate depends on the saturation of hospital capacities; so the confinement has an impact on the death toll too (assuming the coefficient γ to be nonzero and the hospital capacity to be saturated).
In addition, in our model we include confinement duration constraints for each age, more precisely:
 (2.11)
(2.11)
3 Discretization of the control problem
In this section, we present the discrete model associated to the previous formulation. The main objective of this section is to explain how to write the discrete problem so that an optimal control solver (based on an ODE model) can address it (see Appendix A for more details).
For the age a ∈ [0, A] we take discrete values {1, …, na}. As both time unit, time step and discretization of the infection age we choose one day.
The horizon of the problem will be  . Let n0, nb, with n0 < nb be the duration of the incubation phase and of the infection, respectively.
. Let n0, nb, with n0 < nb be the duration of the incubation phase and of the infection, respectively.
The time index is  , starting from value 0. The infection age is j ∈{1, …, nb}. The initial conditions are
, starting from value 0. The infection age is j ∈{1, …, nb}. The initial conditions are
![\begin{equation*} \begin{array}{rcll} y^0_{a}&=&y_0(a) & a=1,\dots, n_a,\\[6pt] z^0_{a,{j}}&=&z_0(a,{j})& a=1,\dots,n_a, \;\; {j} =1,\dots,n_b,\\[6pt] h^0_{a,{j}}&=&h_0(a,{j}) & a=1,\dots, n_a, \;\; {j} =1,\dots,n_b.\\[6pt] \end{array} \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq23.png) (3.1)
(3.1)
The global transmission factor and the size of the hospitalized population are respectively
 (3.2)
(3.2)
Also Ek ∈ [0, 1] is a discrete counterpart to the hospital saturation estimate E(t), given by
 (3.3)
(3.3)
Willing to keep conservation laws, we may write the dynamics as follows: for all a = 1, …, na,
![\begin{equation*} \begin{array}{rcll} y^{k+1}_{a}&=& \left(1 - \delta_a (1-u^k_a) Z^k\right)y^k_{a} & \;\\[6pt] z^{k+1}_{a,1}&=& \delta_a (1-u^k_a) Z^k y^k_a&\;\\[6pt] z^{k+1}_{a,{j}}&=&(1-\nu_{a,{j}-1})z^k_{a,{j}-1}& {j} =2,\dots, n_b\\[6pt] h^{k+1}_{a,1}&=&0&\;\\[6pt] h^{k+1}_{a,{j}}&=& \nu_{a,{j}-1}z^k_{a,{j}-1} + (1-\eta_{a,{j}-1} - \gamma_{a,{j}-1} E^k)h^k_{a,{j}-1}& {j} =2, \dots, n_b\\[6pt] {\bar{y}}^{k+1}_{a}&=&{\bar{y}}^k_{a}+z^k_{a,n_b}+h^k_{a,n_b}. & \; \end{array}\end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq26.png) (3.4)
(3.4)
The death toll per age and day, and per day, are resp.
 (3.5)
(3.5)
The parameters of the dynamics are:
| δa : | transmission rate |
| νa,j: | hospitalization rate |
| ηa,j: | minimal death rate |
| γa,j: | sensitivity of the death rate w.r.t. hospital saturation. |
Remark 3.1.
The state variable 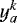 remains nonnegative iff
remains nonnegative iff
In the case of normalized, (i.e., summing to 1) initial population, we have that Zk ≤1. So, the previous nonnegativity condition holds whenever δa ≤ 1. In our numerical test, it may happen that δa ≥ 1, but  always remained positive.
always remained positive.
On the other hand, in our tests ηa,j + γa,j ≤ 1. Since Ek ≤ 1 by definition, it follows that  always remains nonnegative.
always remains nonnegative.
We have the following constraints: maximal achievable confinement, peak value for the hospital capacity, and cumulated confinement effort. Namely, for some ![$u^M_a \in [0,1]$](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq32.png) , M ≥ 0, and Ma ≥ 0:
, M ≥ 0, and Ma ≥ 0:
![\begin{equation*} \begin{array}{l} 0\leq u^k_a\leq u^M_a,\;\;\;k=0,\dots, N, \; a \in \{1,n_a\} \\[6pt] H^k\leq M, \quad k=0,\dots, N,\\[6pt] \sum_{k=0}^{N-1} u^k_a \leq M_a, \; a \in \{1,n_a\}. \end{array}\end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq33.png) (3.7)
(3.7)
The expression of the cost is
 (3.8)
(3.8)
with cu weighted confinement cost, DT total death toll:
 (3.9)
(3.9)
and pu, pM and pD are nonnegative penalty coefficients.
Due to the incubation phase, the value of control for the last n0 days has no influence on the hospitalizations and therefore, neither on the death toll nor on the hospital capacity constraint.
4 Estimation of coefficients and initial state
4.1 Incubation and infectious phases
As we mentioned in Remark 2.1, for our numerical tests we assume that there exists an incubation phase (days 1 to n0 − 1 of infection) where no transmission and hospitalizations occur. So,
 (4.1)
(4.1)
The above assumptions together with the initial condition  implies that
implies that
 (4.2)
(4.2)
During the infectious phase (j varying from n0 + 1 to nb) we may assume that the coefficients νa,j, for j ≥ n0 ηa,j and γa,j, for j ≥ n0 + 1, do not depend on j and therefore are equal to some positive constants  ,
,  ,
,  .
.
We assume that we know for each age the total proportion  of transfers from z to h, that satisfies
of transfers from z to h, that satisfies
 (4.3)
(4.3)
Similarly, we may assume that we know for each age the proportion  of hospitalized people that will die, when the hospital capacity is not saturated. Since
of hospitalized people that will die, when the hospital capacity is not saturated. Since  , for j = 1, …, n0, we have by similar arguments
, for j = 1, …, n0, we have by similar arguments
 (4.5)
(4.5)
As expected,  and
and  take values in [0, 1].
take values in [0, 1].
When the total hospital capacity is exceeded we assume that it can be measured so that  itself can beevaluated.
itself can beevaluated.
4.2 Initial condition
Assuming that we know a growth factor g for the infected population given a time period of p time steps, then epλ = g, so that
 (4.6)
(4.6)
We assume that the initial time corresponds to an early phase of the epidemic, and therefore that the h and ȳ variables are equal to zero, and (since the order of magnitude of y is almost constant) search for the z variable a solution of the form
 (4.7)
(4.7)
We can express ca,j as function of ca,1:
 (4.8)
(4.8)
So the total and infectious population of z for each age are resp.
 (4.9)
(4.9)
 (4.10)
(4.10)
In the absence of confinement at initial time, estimating ca,1 with the previous relation, we deduce the value of δ from:
 (4.11)
(4.11)
As noted in Remark 3.1, in order that yk remains nonnegative, we need that
 (4.12)
(4.12)
Remark 4.1
We have seen that, since the initial time corresponds to an early stage of the epidemic, we can assume that h0 = 0 and ȳ0 = 0, and additionally, we can assume that there is no saturation of the hospital capacity. We could consider that we have statistical estimates of the “initial parameters" λ,
 ,
,
 ,
y0, Z0.
,
y0, Z0.
Then we can deduce  and
and  from (4.4) and (4.5), respectively. The value of χ
and
from (4.4) and (4.5), respectively. The value of χ
and  follow. We can deduce ca,1 from (4.10) and the values of z0 follow with (4.7). Finally, we deduce δ from (4.11).
follow. We can deduce ca,1 from (4.10) and the values of z0 follow with (4.7). Finally, we deduce δ from (4.11).
For the estimate of the γ parameters, specific methods are needed, which are beyond the scope of this paper.
5 Numerical tests
5.1 Choice of parameters and initial conditions
We consider the available data for France up to April 6, 2020. From Santé publique France and data.gouv.fr we obtain the following information:
| Total confirmed cases: | 74 390 |
| Total hospitalized cases: | 54 036 |
| Total confirmed deaths: | 8911 |
From these data we can estimate the values of  and
and  that represent the proportion of infected population in needs of hospitalization and the proportion of deaths with respect to the hospitalizations, respectively.
that represent the proportion of infected population in needs of hospitalization and the proportion of deaths with respect to the hospitalizations, respectively.
 (5.1)
(5.1)
Furthermore, from the above-mentioned sources, we can observe that in the beginning of the epidemic, the growth factor per week is between 2.5 and 3, we can considerthat
![\begin{equation*} \lambda \in [0.13,0.15]. \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq66.png) (5.2)
(5.2)
In the French demographic institute website INED we find detailed information on deaths in hospitals, taking into account the age of the population. We deduce that the strong population y1 can be considered as the population up to 59 years and the weak population y2 as the population over 60 years. In this case, we have
| Total population | % | Total confirmed deaths | % | |
|---|---|---|---|---|
| strong | 49 213 491 | 73.4 | 416 | 6.5 |
| weak | 17 850 240 | 26.6 | 6021 | 93.5 |
| total | 67 063 703 | 100 | 6037 | 100 |
Since they only consider deaths in hospitals, the number of deaths in the two previous tables is not the same. From the last table we can calculate the relative mortality rate as
 (5.3)
(5.3)
which implies that the ratio of this rate is
 (5.4)
(5.4)
In order to obtain the values of  and
and  , we assume that ratio is the same, i.e.,
, we assume that ratio is the same, i.e.,  . Normalizing the population, the global death rate
. Normalizing the population, the global death rate  is equal to
is equal to
 (5.5)
(5.5)
By (5.1) we obtain,
 (5.6)
(5.6)
Since we do not have detailed information about the age of hospitalized people, we assume:
 (5.7)
(5.7)
Finally, from data.gouv.fr we know the total of confirmed cases per day, but again we do not have the information by age. For this reason, and since in our formulation, the discount term in the first dynamics equation is depending on the sum of infected population (Zk), we consider that if  is the initial confirmed cases, then we can define the (normalized) initial confirmed cases by age, as
is the initial confirmed cases, then we can define the (normalized) initial confirmed cases by age, as
 (5.8)
(5.8)
where y0 = 6 706 3703 is the total population of France.
Since we have taken the same values of  for the two populations, and the initial infected population proportional to the total population, the values for δ are identical. The initial infected population is computed as it was explained, taking the data from data.gouv.fr.
for the two populations, and the initial infected population proportional to the total population, the values for δ are identical. The initial infected population is computed as it was explained, taking the data from data.gouv.fr.
In our numerical tests, the first day is March 15, 2020. For France this was actually the first day of confinement, with 6633 confirmed cases. We consider the following parameters:
 |
Initial strong population | 0.734 |
 |
Initial weak population | 0.266 |
 |
Initial infected strong population | 7.26e − 5 |
 |
Initial infected weak population | 2.63e − 5 |
| λ | Growth coefficient given by (4.6) | 0.13 |
 |
Total proportion of transfers from z1 to h1 | 0.726 |
 |
Total proportion of transfers from z2 to h2 | 0.726 |
 |
Strong minimal death rate | 0.014 |
 |
Weak minimal death rate | 0.58 |
We choose an incubation duration of 6 days, and a total infection duration as 14 days. From the above table, following the methodology described in Remark 4.1, we obtain:
![\begin{equation*} \begin{array}{lll} \delta_1=1.656, &\; {\bar{\nu}}_1=0.149412, &\; {\bar{\eta}}_1=0.002012\\[6pt] \delta_2=1.656, &\; {\bar{\nu}}_2=0.149412, &\; {\bar{\eta}}_2= 0.116557 \end{array} \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq79.png) (5.9)
(5.9)
In addition, we assume:
 (5.10)
(5.10)
5.2 Numerical results in the case of an age independent control
In these first four tests, we assume the control variables to be independent of the age a, i.e.,  for all k, that the upper bound for the control is uM = 0.75, and that the confinement cost, given by (3.9), satisfies ce,1 + ce,2 = 1. We present different scenarios, taking different penalty terms in the objective function. We do not consider any cumulated control constraints.
for all k, that the upper bound for the control is uM = 0.75, and that the confinement cost, given by (3.9), satisfies ce,1 + ce,2 = 1. We present different scenarios, taking different penalty terms in the objective function. We do not consider any cumulated control constraints.
In each of the figures below, we show four graphics. The first one (upper left), is the optimal confinement, the second one (upper right) is the cumulative number of deaths for the strong and weak population, the third one (bottom left) is the number of people in need of hospitalization per day and the last one (bottom right) shows the evolution of the susceptible strong and weak population.
Test 1: pM = 1, pu = 1, pD = 1, Figure 1.
Test 2: pM = 1, pu = 0.000001, pD = 0, Figure 2
Test 3: pM = 1e − 5, pu = 0, pD = 1, Figure 3
Test 4: pM = 1, pu = 0.0005, pD = 1, Figure 4
 |
Figure 1 Test 1: pM = 1, pu = 1, pD = 1. The optimal control is 0. Without confinement, the death toll is greater than 10% and the peak value is very large, as expected. |
 |
Figure 2 Test 2: pM = 1, pu = 0.000001, pD = 0. In this case, the main objective is to reduce the peak value. We can observe the delay, between the confinement decision and the response in the hospitalized population. Indeed, when the confinement stops, the size of hospitalized population remains constant for several days. The death toll is greater than 10%. |
 |
Figure 3 Test 3: pM = 1e − 5, pu = 0, pD = 1. The main objective is to reduce the death toll, without considering the confinement cost. Therefore, the optimal policy assumes themaximum confinement value until the last days. Since the saturation of hospital capacity impacts in the death rate, as a consequence the peak value is reduced. |
 |
Figure 4 Test 4: pM = 1, pu = 0.0005, pD = 1. In this case,we want to reduce the peak value and the death toll, taking into account the economic impact. |
In the following table we show the death toll for strong, weak and total population, follow by  and the peak value M.
and the peak value M.
| Test | D1,T | D2,T | DT | I(u) | M |
|---|---|---|---|---|---|
| 1 | 0.0088192 | 0.116966 | 0.1257852 | 0 | 0.27665 |
| 2 | 0.00816993 | 0.111278 | 0.11944793 | 54.49 | 0.0698543 |
| 3 | 0.00660044 | 0.0906906 | 0.09729104 | 102.375 | 0.0693109 |
| 4 | 0.00688871 | 0.094924 | 0.10181271 | 65.9702 | 0.0715698 |
Discussion of the numerical results for an age independent control:
To analyze and compare the complete behavior of the epidemic when different confinement policies are applied, we assume that the maximum for this control is 0.75. Of course, this is the reason why in the tests we obtain that almost the entire population is immunized in the period considered. On the contrary, at the moment in France and in many countries around the world, containment measures are stronger and after more than amonth of confinement we are far from the end of the epidemic. If these policies continue, the time needed to reach this level of immunization will be even longer.
From the above tests, we can observe that if there is no confinement, which is the case of Test 1, then the health system will collapse andthe death toll will be very large, as expected.
It is interesting to compare Test 2 and Test 3. In Test 3, the main objective is to reduce the death toll, and we observe that in comparison with Test 2, we obtain more or less the same peak, some days after, but with a small death toll. The difference between them, is that in the first case, when the hospitalized population attains its maximum, the confinement stops, whereas in Test 3, the confinement is maximal until the end. That means that reducing the peak is not enough to reduce the final number of deaths.
Finally, as expected, in Test 4 since the control penalty is greater than those previously considered, the confinement is reduced, obtaining a greater peak value and death toll, but even though the death toll is smaller than in Test 2. We can also observe thatin Test 4 since the optimal policy is 0 during the first 20 days, the peak value is obtained several weeks before than in Test 2 and Test 3.
As we mentioned in the introduction, it is very difficult to weigh economic losses against the number of lives lost.
5.3 Numerical results with age dependent controls
Taking into account these results, it is clear that most deaths occur in the weak population, so it is natural to address the issue of considering two different levels of confinement, depending on the age of the population. We take 0.75 as upper bound for the two confinement controls. In this case, the cost function is given by (3.9). For the numerical tests, we assume that ce,1 = 0.734 and ce,2 = 0.133. With this coefficients we take into account the proportion of the population that is weak and strong and we also assume that confinement for the elderly has less impact on the economy than confinement for the young. We use the same initial conditions and parameters as in the previous tests. For Test 5 and Test 6, we do not consider any cumulated control constraints.
Test 5: pM = 1, pu = 0.000001, pD = 0, Figure 5
 |
Figure 5 Test 5: pM = 1, pu = 0.000001, pD = 0. Since hospitalizations rates |
Test 6: pM = 1, pu = 0.0005, pD = 1, Figure 6
 |
Figure 6 Test 6: pM = 1, pu = 0.0005, pD = 1. As in Test 4, the aim is to balance between reducing peak value, death toll and confinement cost. We observe an important difference between optimal confinement for strong and weak populations. Of course, this occurs due to the difference between the mortality rates for both populations. |
In the last test, we take the same values of Test 6, but we include cumulated control constraints (3.7) with M1 = 25 and M2 = 45.
Test 7: pM = 1, pu = 0.0005, pD = 1, Figure 7
 |
Figure 7 Test 7: pM = 1, pu = 0.0005, pD = 1, with the confinement lengths M1 = 25 and M2 = 45. The objective of this test is to show how the optimal policy changes when we add constraints in the confinement lengths. Taking the delay into account, we see that the end of confinement of the strong population corresponds to the end of the hospitalization peak. |
In the following table, we summarized the results of the tests with differentiated confinement:
| Test | D1,T | D2,T | DT | I(u1) | I(u2) | M |
|---|---|---|---|---|---|---|
| 5 | 0.00817212 | 0.109833 | 0.11800512 | 67.7524 | 73.6568 | 0.0693917 |
| 6 | 0.00824508 | 0.0983062 | 0.10655128 | 35.8425 | 62.25 | 0.0729996 |
| 7 | 0.00837618 | 0.10037 | 0.10874618 | 25 | 45 | 0.0805676 |
Discussion of the numerical results for age dependent controls:
We analyze the difference between taking a confinement policy dependent or independent of the age. Test 5 is similar to Test 2, in both cases we achieve to reduce the peak value, but we obtain a very high death toll. In Test 5, there is no significant difference between confinement for the strong and weak population, and the behavior is similar to Test 2, once the peak is reached, theconfinement stops (taking into account the delay effects).
The comparison between Test 4 and Test 6 is maybe the most interesting one. With similar penalty terms, we obtain almost the same death toll and peak value. The main difference is that the strong population has a considerably shorter confinement in Test 6, while the weak population has almost the same as in Test 4. This confirms that performing differentiated confinement is perhaps the best response when seeking to minimize the economic impact of confinement, while at the same time reducing the number of deaths.
From the available data, it is evident that the majority of deaths belong to the weakest group, so it is natural to think that if the objective is to reduce the number of final deaths, the confinement for this group should be larger than for the other. When the sole objective is to reduce the peak, we do not observe this behavior because it is more important to reduce the number of infected people than the total number of deaths. Since in our model we take into account the saturation of the hospital system in the mortality rate of hospitalized people, when we minimize the number of deaths, we also obtain a reduction in the peak.
5.4 Two cases of specific interest
As we mentioned in the previous discussions, the objective of the previous tests was to analyze different scenarios that show that our numerical methods work well and that all the results obtained are consistent with our model. Now we will try to analyze cases closer to thecurrent data.
5.4.1 A quasi-periodic control
In order to show an example which may be closer to the actual available data so far in France, we consider the case when after March 15, the transmission rate δ is reduced to the half. This can be interpreted as a result of a change in the population behavior, in addition to the confinement policy itself, such as washing hands, social distancing, and the use of masks. We allow the confinement policy to take values between 0 and 0.9. We choose pM = 12, pu = 0.005, pD = 1 and assume that the hospital capacity is C = 0.01. See Figure 8.
After several weeks of confinement, hospitalizations per day begin to decrease. As expected, since the total number of immunized people is still too small, the epidemic is far from the end and when the confinement policy is relaxed, a rebound can be observed. This quasi-periodic feature of confinement could be a good strategy not to overwhelm the health system.
Given that the containment policy is very strong, after 140 days we did not observe great changes in the number of immunized people. However, the death toll is close to 0.0011, which is equivalent to approximately 73,000 people. Again, the reason for this large number of deaths is due to the hospitalization and mortality rates considered.
 |
Figure 8 Quasi-periodic case: pM = 12, pu = 0.005, pD = 1, C = 0.01. |
5.4.2 Long-term behavior
In this case, we take the parameters values of the above test, in particular the transmission rate δ = 0.825 and the control takes values in [0, 0.9]. The penalty terms are pM = 12, pu = 0.005, pD = 1, which implies that the main objective is to reduce the peak value, taking into account the death toll, but the costs associated with confinement are quite high. In this test we increase the horizon to 260 days.
We observe that some days after the peak of hospitalizations is achieved, the control is very high, and then it begins to slowly decrease to zero, which is when the epidemic is close to ending, see Figure 9. When the situation of the country does not allow to take a long and strong confinement, this may be the more accurate strategy. Of course, due to penalties considered, the death toll is still too high.
 |
Figure 9 Long-term behavior: pM = 12, pu = 0.005, pD = 1, C = 0.01, T = 260. |
5.5 Comments on the numerical results
A critical question is to check if data are available for evaluating the coefficients. Exchanges on the model with epidemic experts would be of course very useful.
We want to point out that all the results obtained in the tests are illustrative. It is well known that the available data on confirmed cases could be far from the actual number, due to asymptomatic cases. A higher number of infected people would imply that hospitalization and mortality rates are lower and, therefore, the death toll as well as the maximum number of hospitalizations will be lower. In fact, we took the available data on March 15, 2020, when the death toll was almost 16%. This is why,in our tests, when the epidemic is almost over, the number of deaths is so high.
In addition, the other parameter that influences the number of deaths and the peak value, is the hospitalization rate  , which at the beginning was close to 70%. Given that there are apparently many cases that are not serious, at a later stage of the epidemic when there is more demand in hospitals, some of these cases could be treated at home, obtaining a lower rate. Furthermore, we have no information on the length of hospitalization.
, which at the beginning was close to 70%. Given that there are apparently many cases that are not serious, at a later stage of the epidemic when there is more demand in hospitals, some of these cases could be treated at home, obtaining a lower rate. Furthermore, we have no information on the length of hospitalization.
6 Conclusion
6.1 Possible extensions
We want to highlight several possible extensions or modifications of our model. Of course, such changes require further information, but we may have more accurate data in the near future. For instance, if a vaccine is available we can introduce a new control v(t, a) which is the per capita rate of vaccination. The resulting modification in the dynamics would be:
 (6.1)
(6.1)
It is natural to think that v depends on the age of the population, and the limitation of MV vaccines per day would read as
 (6.2)
(6.2)
Here, we neglect any delay for the vaccination to become effective. Also, if data was available, it may be useful to split the infected population between the confirmed cases (taking advantage of a testing policy) and non-confirmed (among then some asymptomatic cases). Keeping the variable z for the non-confirmed cases, we could introduce a new state w(t, a, b) representing the confirmed cases. Assuming the latter to be isolated, only the z population contributes to the global transmission factor Z(t). We obtain the following dynamics:
![\begin{equation*} \left\{\begin{array}{l} \dot{y}(t,a)=-\delta(a)(1-u(t,a))Z(t)y(t,a)\\[6pt] (z_t+z_b)(t,a,b)=-\mu(t,a,b)z(t,a,b)-\nu(a,b)z(t,a,b)\\[6pt] (w_t+w_b)(t,a,b)=\mu(t,a,b)z(t,a,b)-\nu(a,b)w(t,a,b)\\[6pt] (h_t+h_b)(t,a,b)=\nu(a,b)(z(t,a,b)+w(t,a,b))-\left(\eta(a,b) + \gamma(a,b) E(t)\right) h(t,a,b)\\[6pt] \dot{{\bar{y}}}(t,a)=z(t,a,B)+w(t,a,B)+h(t,a,B). \end{array} \right. \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq86.png) (6.3)
(6.3)
Here μ(t, a, b) ≥ 0 is another control, which represents the detection rate. A possible associated cost for the testing policy would be, for some positive coefficients c1 and c2:
 (6.4)
(6.4)
In addition, we can consider the hospitalization age to be a significant parameter. Denoting it by c ∈ [0, C], and assuming that h depends on (t, a, c), we get the following dynamics for the hospitalized population:
![\begin{equation*} \left\{ \begin{array}{l} h(t,a,0)=\int_0^b \nu(a,b)(z(t,a,b)+w(t,a,b)) \textrm{d} b\\[6pt] (h_t+h_c)(t,a,c)=-\left(\eta(a,c) + \gamma(a,c) E(t)\right) h(t,a,c), \;\;\; c\in [0,C]. \end{array} \right. \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq88.png) (6.5)
(6.5)
It is also possible to introduce a recovery rate, that could depend on the hospitalization age, and would contribute to the dynamics of ȳ.
As we can see there are many possible adaptations of our model. On the other hand, one should avoid to excessively increase the number of states and parameters. A model with too many states is difficult to optimize; one with too many parameters makes identifiability uneasy.
6.2 Final remarks
Population models with infection age need (after infection age discretization) many states. Nevertheless, we could obtain a numerical convergence of our solvers in various cases. Sometimes we needed to solve the problem first with a small horizon (e.g. 3 months) and then to increase progressively the horizon, in order to obtain the convergence.
The main advantage of our model is the age-structure. Despite the limited accuracy of the parameters and the obtained data, in our tests we recovered the particular behavior of the epidemic with respect to the incubation phase and almost fixed duration, at least for non-severe cases. We can see the delay in the response when a containment policy is taken, which is crucial in this type of disease where the infected population grows exponentially.
Our model is quite flexible and allows to take for instance variable coefficients during or after the incubation phase. In future studies one should of course take advantages of clinical studies in order to take into account a more accurate dynamical model, including the response to drugs, as well as the extensions just previously discussed.
It is of interest to observe how is the containment variable in the “long term” case of Section 5.4.2. The containmentis initially absent, then close to its maximal value at a time close to the saturation of the hospital capacity, then smoothly decreases and goes back to 0. This (happily) seems to be in accordance with the expected social behavior (to accept more easily strict measures at the beginning).
Besides, this study raises interesting questions related to the analysis of the optimality conditions, especially since the model involves state constraints. For this purpose the techniques of the recent paper [3] could be useful.
Appendix A General time steps
We used the open-source optimal control solver Bocop ([2], http://www.bocop.org). Since our software solves optimal control problems described by an ODE, the present problem does not enter in its format. However, note that we can rewrite the discrete system (3.4) in this way:
![\begin{equation*} \begin{array}{rcl} y^{k+1}_{a} - y^k_{a}&=& - \delta_a (1-u^k_a) Z^ky^k_{a} \\[6pt] z^{k+1}_{a,1} - z^k_{a,1}&=& -z^k_{a,1} + \delta_a (1-u^k_a) Z^k y^k_a\\[6pt] z^{k+1}_{a,{j}} - z^k_{a,{j}}&=& -z^k_{a,{j}}+(1-\nu_{a,{j}-1})z^k_{a,{j}-1}\\[6pt] h^{k+1}_{a,{j}} - h^{k}_{a,{j}}&=& -h^{k}_{a,{j}} + \nu_{a,{j}-1}z^k_{a,{j}-1} + (1-\eta_{a,{j}-1} - \gamma_{a,{j}-1} E^k) h^k_{a,{j}-1}\\[6pt] {\bar{y}}^{k+1}_{a} - {\bar{y}}^k_{a} &=& z^k_{a,n_b}+h^k_{a,n_b}. \end{array}\end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq89.png) (A.1)
(A.1)
Taking advantage of the fact that the time step is 1, we see that the discrete system (3.4) can be interpreted as the explicit Euler discretization scheme, for dynamics corresponding to the r.h.s. of the above array.
While a time step of one day is natural, in the case of large horizons it may be useful to conduct experiments with time steps of several days. So, consider a time step (equal to the step for the infection age) Δ > 0. We need  to be integer. Clearly the following system is a consistent approximation of (2.1):
to be integer. Clearly the following system is a consistent approximation of (2.1):
![\begin{equation*} \begin{array}{rcl} \displaystyle \frac{y^{k+1}_{a} - y^k_{a}}{\UpDelta}&=& - \delta_a (1-u^k_a) Z^ky^k_{a} \\[6pt] \displaystyle \frac{z^{k+1}_{a,1} - z^k_{a,1}}{\UpDelta}&=& \displaystyle \frac{-z^k_{a,1}}{\UpDelta} + \delta_a (1-u^k_a) Z^k y^k_a\\[6pt] \displaystyle \frac{z^{k+1}_{a,j+1} - z^k_{a, j+1}}{\UpDelta}&=& \displaystyle \frac{z^k_{a,{j}}-z^k_{a,j+1}}{\UpDelta}-\nu_{a,j-1}z^k_{a,{j}}\\[6pt] \displaystyle \frac{h^{k+1}_{a,j+1} - h^{k}_{a,j+1}}{\UpDelta}&=& \displaystyle \frac{h^k_{a,{j}}-h^{k}_{a,j+1}}{\UpDelta} + \nu_{a,j}z^k_{a,j} - (\eta_{a,j} + \gamma_{a,j} E^k) h^k_{a,j}\\[6pt] \displaystyle \frac{{\bar{y}}^{k+1}_{a} - {\bar{y}}^k_{a}}{\UpDelta} &=& z^k_{a,n'_b}+h^k_{a,n'_b}. \end{array} \end{equation*}](/articles/mmnp/full_html/2020/01/mmnp200165/mmnp200165-eq91.png) (A.2)
(A.2)
In addition the above scheme is conservative, and can be interpreted as the explicit Euler discretization scheme, for dynamics corresponding to the r.h.s.
References
- B. Ainseba, S. Aniţa and M. Langlais, Optimal control for a nonlinear age-structured population dynamics model. Electron. J. Differ. Equ. 9 (2003) 28. [Google Scholar]
- J. Bonnans, D. Giorgi, V. Grélard, B. Heymann, S. Maindrault, P. Martinon, O. Tissot and J. Liu, Bocop – a collection of examples. Technical report, INRIA (2017). [Google Scholar]
- J.F. Bonnans and J. Gianatti, Optimal control of state constrained age-structured problems. SIAM J. Control Optim. 58 (2020) 2206–2235. [Google Scholar]
- M. Brokate, Pontryagin’s principle for control problems in age-dependent population dynamics. J. Math. Biol. 23 (1985) 75–101. [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- R. Djidjou-Demasse, Y. Michalakis, M. Choisy, M.T. Sofonea and S. Alizon, Optimal COVID-19 epidemic control until vaccine deployment. Preprint MedRxiv: 20049189v2 (2020). [Google Scholar]
- R. Elie, E. Hubert and G. Turinici, Contact rate epidemic control of covid-19: an equilibrium view. MMNP 15 (2020) 35. [EDP Sciences] [Google Scholar]
- W.O. Kermack, A.G. McKendrick and G.T. Walker, A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. Lond. A 115 (1927) 700–721. [CrossRef] [Google Scholar]
- Q. Lin, S. Zhao, D. Gao, Y. Lou, S. Yang, S.S. Musa, M.H. Wang, Y. Cai, W. Wang, L. Yang and D. He. A conceptual model for the coronavirusdisease 2019 (covid-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 93 (2020) 211–216. [CrossRef] [PubMed] [Google Scholar]
- Z. Liu, P. Magal, O. Seydi and G. Webb, Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. Preprint MedRxiv: 20034314v1 (2020). [Google Scholar]
- Z. Liu, P. Magal, O. Seydi and G. Webb, Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology 9 (2020) 50. [Google Scholar]
- H. Maurer and M. do Rosario de Pinho, Optimal control of epidemiological SEIR models with L1-objectives and control-state constraints. Pac. J. Optim. 12 (2016) 415–436. [Google Scholar]
- Q. Richard, S. Alizon, M. Choisy, M.T. Sofonea and R. Djidjou-Demasse, Age-structured non-pharmaceutical interventions for optimal control of covid-19 epidemic. Preprint MedRxiv: 20138099v1 (2020). [Google Scholar]
- C. Silva, H. Maurer and D. Torres, Optimal control of a tuberculosis model with state and control delays. Math. Biosci. Eng. 14 (2017) 321–337. [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
All Figures
 |
Figure 1 Test 1: pM = 1, pu = 1, pD = 1. The optimal control is 0. Without confinement, the death toll is greater than 10% and the peak value is very large, as expected. |
| In the text | |
 |
Figure 2 Test 2: pM = 1, pu = 0.000001, pD = 0. In this case, the main objective is to reduce the peak value. We can observe the delay, between the confinement decision and the response in the hospitalized population. Indeed, when the confinement stops, the size of hospitalized population remains constant for several days. The death toll is greater than 10%. |
| In the text | |
 |
Figure 3 Test 3: pM = 1e − 5, pu = 0, pD = 1. The main objective is to reduce the death toll, without considering the confinement cost. Therefore, the optimal policy assumes themaximum confinement value until the last days. Since the saturation of hospital capacity impacts in the death rate, as a consequence the peak value is reduced. |
| In the text | |
 |
Figure 4 Test 4: pM = 1, pu = 0.0005, pD = 1. In this case,we want to reduce the peak value and the death toll, taking into account the economic impact. |
| In the text | |
 |
Figure 5 Test 5: pM = 1, pu = 0.000001, pD = 0. Since hospitalizations rates |
| In the text | |
 |
Figure 6 Test 6: pM = 1, pu = 0.0005, pD = 1. As in Test 4, the aim is to balance between reducing peak value, death toll and confinement cost. We observe an important difference between optimal confinement for strong and weak populations. Of course, this occurs due to the difference between the mortality rates for both populations. |
| In the text | |
 |
Figure 7 Test 7: pM = 1, pu = 0.0005, pD = 1, with the confinement lengths M1 = 25 and M2 = 45. The objective of this test is to show how the optimal policy changes when we add constraints in the confinement lengths. Taking the delay into account, we see that the end of confinement of the strong population corresponds to the end of the hospitalization peak. |
| In the text | |
 |
Figure 8 Quasi-periodic case: pM = 12, pu = 0.005, pD = 1, C = 0.01. |
| In the text | |
 |
Figure 9 Long-term behavior: pM = 12, pu = 0.005, pD = 1, C = 0.01, T = 260. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.