| Issue |
Math. Model. Nat. Phenom.
Volume 15, 2020
Coronavirus: Scientific insights and societal aspects
|
|
|---|---|---|
| Article Number | 75 | |
| Number of page(s) | 34 | |
| DOI | https://doi.org/10.1051/mmnp/2020043 | |
| Published online | 15 December 2020 | |
A discrete epidemic model and a zigzag strategy for curbing the Covid-19 outbreak and for lifting the lockdown
1
Université Paris-Saclay, UVSQ, Laboratoire de Mathématiques de Versailles,
78000
Versailles, France.
2
Pacific Institute for the Mathematical Sciences (PIMS), Department of Mathematics and Statistics, University of Victoria,
Victoria,
British Columbia, Canada.
* Corresponding author: tahar.boulmezaoud@uvsq.fr
Received:
3
May
2020
Accepted:
29
October
2020
This study looks at the dynamics of a Covid-19 type epidemic with a dual purpose. The first objective is to propose a reliable temporal mathematical model, based on real data and integrating the course of illness. It is a daily discrete model with different delay times, and whose parameters are calibrated from the main indicators of the epidemic. The model can be broken down in two decoupled versions: a mortality-mortality version, which can be used with the data on the number of deaths, and an infection-infection version to be used when reliable estimates of infection rate are available. The model allows to describe realistically the evolution of the main markers of the epidemic. In addition, in terms of deaths and occupied ICU beds, the model is not very sensitive to the current uncertainties about IFR. The second objective is to study several original scenarios for the epidemic’s evolution, especially after the period of strict lockdown. A coherent strategy is therefore proposed to contain the outbreak and exit lockdown, without going into the risky herd immunity approach. This strategy, called zigzag strategy, is based on a classification of the interventions into four lanes, distinguished by a marker called the daily reproduction number. The model and strategy in question are flexible and easily adaptable to new developments such as mass screenings or infection surveys. They can also be used at different geographical scales (local, regional or national).
Mathematics Subject Classification: 92D30 / 92D25 / 92B05 / 37M05 / 37N25
Key words: Covid-19 pandemic / lockdown / zigzag strategy / deconfinement / epidemic model / daily reproduction number
© The authors. Published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The Covid-19 epidemic we are witnessing today has spread at a phenomenal rate. Leaving China at the end of 2019 (see [52]), it reached almost all the countries of the world within four months. The speed of circulation of the virus Sars-CoV-2 and the short development time of Covid-19 disease leave little time to react. In late April 2020, the epidemic has already absorbed, even saturated, the hospital capacities of many countries, causing more than 200,000 deaths worldwide and seriously affecting the health of at least a million people. The time of circulation and action of the coronavirus Sars CoV-2 appears to be much shorter than the different reaction times of human institutions, whether they are hospital, industrial, scientific or political.
Therefore, to understand the dynamics of a Covid-19 type epidemic, it is necessary to look at the action time of the virus and the disease it causes. Mathematical models that aim to predict these dynamics must take into account clinical times from infection to recovery or to death. More specifically, durations of incubation and of contagiousness period, time from onset to admission in ICU (Intensive Care Unit) and time from onset to death or discharge, are all important parameters that must be estimated and integrated into the model (see, e.g., [32]).
However, in the face of urgency, scientists cannot rely solely on complex computational models, whose implementation, responsiveness, and needs in data require weeks of data collection and prohibitive calculation costs.
Paradoxically, the importance of chronological aspects in understanding the epidemic potential of this virus could lead to mathematical models that are less costly in terms of computing time and data collection. Indeed, the space variable, although important, does not play a major role in its spread: the virus does not spread by a wave that moves slowly from region to region, but by the multiplication of clusters and epidemic foci. Thus, models that rely on systems of partial differential equations where the space variable lives in a continuum may not be adequate for this epidemic. Moreover, it is now generally accepted that the age is a risk factor (see, e.g., [45, 51]). It can therefore be deduced that this leads to population behaviors that differ with age, causing variability in transmission. However, the influence of age on transmission is still unclear (see [8, 15], etc.). For this reason, most existing epidemiological models for respiratory virus epidemics initially focus on temporal aspects. Age and spatial structuring generally takes place in a second stage, with the aim of refining the models so that they are as close as possible to reality.
There are many deterministic or stochastic mathematical models that describe the evolution of an epidemic. The most successful are time-continuous deterministic compartmentalized models. Often inspired by Kermack-McKendrick’s SIR model [25] (see also [3]), these models generally consist in a repartition of individuals into several epidemiological classes. The dynamics of this repartition is described by a system of inter-coupled differential equations. As indicated in [21], there are a large number of these compartmentalized models (see for example [4, 5, 9, 20, 23, 24, 31, 40]). In addition, there is another family of so-called stochastic models that have been developed in parallel with deterministic models. One can cite the Reed-Frost model (see [1]), Greenwood model [18] or other later models (see [6, 7, 11, 46]). We can also mention agent-based models that aim to take into account all heterogeneities by mimicking the behaviour of individuals as closely as possible (see [17, 22, 34, 44]).
The reader interested in all these models can consult the works of Anderson and May [2], Brauer and Castillo-Chávez [9], Diekmann and Heesterbeek [13], Britton and Pardoux [10] or Thieme [42]. It should be noted that many developments or adaptations of these classical models have been introduced very recently, during the current Covid-19 pandemic. It is too early to make an exhaustive description and evaluation of all these developments.
Furthermore, one of the difficulties encountered in the study of this pandemic stems from the collected data, particularly those concerning the number of infected individuals. Many people are infected without developing severe clinical manifestations of the disease, while at the same time becoming contagious. In addition, the difficulty of performing virological tests in large numbers is leading to a refocusing of screening on cases who have severe illness symptoms. It is therefore unreasonable at this stage to base models solely on the number of detected or confirmed cases as the only indicator, unless the number of unreported or asymptomatic cases is included in these models [19, 31]. Even the proportionality the number of detected cases to the total number of infected cases is not guaranteed, because of the continuous evolution of screening capacities and public policies. On the other hand, it could be accepted without difficulty that mortality (or in-hospital mortality), admission to intensive care units, or even hospitalizations, are markers that reflect the evolution of the pandemic in a much more specific way.
Taking all these observations into account, we propose here a discrete deterministic model for forecasting the temporal evolution of the epidemic from day to day, taking into account the different medical parameters that characterize it. It is a decoupled model in which mortality is predicted from mortality data only, and which makes it possible to simulate the evolution under several scenarios of various other indicators such as the number of occupied ICU beds, the number of infected or recovered cases, and the number of active cases. The fact that these predictions are based primarily on mortality data makes the model less sensitive to the IFR (Infection Fatality Ratio), especially in realistic phases of the epidemic (the IFR will be used primarily to deduce the numbers of infected, recovered or active cases from the death numbers). This model makes it possible to monitor the impact of restrictive interventions and the behavior of individuals. It can also predict the short- and long-term dynamics of the epidemic, according to several scenarios. The state of the epidemic in France will be particularly examined.
The model has a number of parameters. These are mainly the daily reproduction number (to be distinguished from the basic reproduction number), transmission coefficients, and certain time delays. The transmission coefficients are calibrated from data using an inverse method (without making additional assumptions about the contagiousness profile). Time delays are inferred from clinical data. As for the daily reproduction number, introduced here, it is a dynamic marker thatcan be measured from the data and allows the impact of the public interventions to be assessed. It will play a fundamental role in predicting the course of the epidemic under different scenarios, and in designing a technique to control it without maintaining permanent drastic interventions. This technique, called zigzag strategy, consists of alternating periods of strict lockdown and moderate deconfinement according to precise rules.
The remaining of this paper is oraganized as follows: in Section 2, we expose the main features of the model. For reasons of readability, its formal justification has been moved to the Appendix A.1. Section 3 is dedicated to the calibration of its various parameters (time delays, transmission coefficients, etc). Section 4 deals with the study of the daily reproduction number in the case of several countries. Section 5 includes the analysis of about ten scenarios for the lockdown exit, by choosing the example of France. These scenarios are all replicable for other countries or for a specific region. The scenario of non-application of lockdown is also studied. In Section 6, the zigzag strategy for controlling the outbreak is outlined. Section 7 is devoted to conclusions.
The reader not interested in the mathematical aspects of the model can simply read Sections 5, 6, 7 and possibly 4.
Finally, it should be noted that the rigorous mathematical study of the model is postponed to another work. Here, the emphasis is deliberately placed on modelling and prediction in the context of realistic scenarios.
2 Model and its parameters
In severe epidemic situations such as the Covid-19 epidemic, many countries adopt daily reporting of infection, hospitalization and mortality indicators. Therefore, the unit of time chosen here is the day. Here  designates an entity with a sufficiently large population. Such an entity can be a given region, a country or a set of countries. However, we can keep in mind, without losing generality, that the reference entity here is the country. We note P the initial size of its population.
designates an entity with a sufficiently large population. Such an entity can be a given region, a country or a set of countries. However, we can keep in mind, without losing generality, that the reference entity here is the country. We note P the initial size of its population.
In this model, we follow the evolution of the epidemic day by day, starting from a certain date J0. This date could depend on the country chosen for the study. We denote  the sequence of subsequent days. For all n ≥ 0, we denote by
the sequence of subsequent days. For all n ≥ 0, we denote by
-
Sn the number of susceptible individuals at the end of the n-day,
-
In the number of infected individuals after the first n days (In includes in particular individuals who have recovered or died),
-
Dn the total number of deaths due to the epidemic that occurred in the first n days,
-
Rn the number of individuals recovered after the first n days,
-
An the number of individuals who were admitted in ICU the first n days (due to the epidemic), even if they have already left these units,
-
 the number of occupied ICU beds at the end of the n-day (by patients affected by the epidemic). Thus,
the number of occupied ICU beds at the end of the n-day (by patients affected by the epidemic). Thus,  refers to the number of people who stayed in the ICU and left it before the end of the nth day.
refers to the number of people who stayed in the ICU and left it before the end of the nth day.
Let us specify from now on that in the whole model the number of deaths Dn can be replaced by the number of deaths in hospital. The model will remain the same (provided that the mortality rate is adjusted, especially when the epidemic is amplified). It will be seen that it is not necessary to know all these indicators at the beginning of the epidemic. Recent data are sufficient to predict what will happen next.
For convenience, we set Dk = Ak = Rk = 0 for any integer k ≤ 0 and Ik = 0 for k < 0. Thus, I0 represents the number of individuals infected on day J0. We also set
 (2.1)
(2.1)
In other words, in and dn represent the number of infections and deaths that occurred on day Jn, respectively, while an represents the number of individuals admitted in ICU on the day Jn. We have the obvious relationships for any n ≥ 0
 (2.2)
(2.2)
Let us summarize the proposed model for studying the evolution of the epidemic. Its justification is postponed to Appendix A.1. In the full version of the model, the dynamics of the number of deaths is governed by the decoupled law (mortality-mortality):
 (2.3)
(2.3)
where Dn−1 is calculated from dk, 1 ≤ k ≤ n − 1, by the relation (2.2), and
-
ℓ ≥ 1 refers to the observed average duration of contagiousness (days),
-
m ≥ 1 refers to the minimum time from infection to contagiousness (days),
-
r ≥ 1 is the average time from illness onset to death,
-
α is the infection fatality ratio (IFR) (or the infection in-hospital fatality rate if Dn denotes the number of deaths in hospital that occurred in the first n days),
-
λ0, ⋯, λℓ−1 are nonnegative transmission coefficients independent of n satisfying
![\[ \sum_{k=0}^{\ell-1} \lambda_k = 1. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq8.png)
Qualitatively, the transmission coefficients λ0, ⋯, λℓ−1 describe the contagiousness of an infected individual (during the m + ℓ days following his infection). They depend in part on the evolution of his viral load. They are estimated from actual data using a least-squares technique explained in Appendix A.2.
In (2.3), for any integer n ≥ 1, Cn designates a nonnegative coefficient that we will call daily reproduction number on day n. This factor depends on the interventions; it decreases when interventions are applied to curb the epidemic, and increases when these interventions are relaxed. We will remember that a sufficient condition to ensure a rapid decline in the epidemic is to keep the constant Cn below 1. An estimate of this factor will be given in the absence of interventions and in periods of strict lockdown, and its evolution in different countries will be compared.
We can observe that the parameter Cn intervenes in the model (2.3) with a delay of r days. This delay is justified by the time from the application of interventions to their impact on mortality figures.
We also notice that the model (2.3) is a non-linear convolutional model. It is this model that we will adopt in the following and that we will complete with the identities to calculate the other indicators. However, it can be linearized if we look at the early stages of the epidemic, when the number of infections remains small compared to the population size. In the latter case we obtain the linearized convolutional model
 (2.4)
(2.4)
The latter identity does not involve mortality rate α. In other words, to predict the evolution of mortality in the early stages of the epidemic only a calibration of transmission coefficients λ0, ⋯, λk and an estimation of daily reproduction numbers Cn are necessary. In addition, this linearized model does not require knowledge of the initial number of infections or deaths. After calibration of the coefficients, the prediction of mortality on day n can be made from the actual mortality data on the (m + ℓ) days preceding it.
We now show how we calculate the number of infected individuals and of occupied ICU beds. These two quantities are linked to Dn by the identities
 (2.5)
(2.5)
 (2.6)
(2.6)
where t is the average time from infection to admissionto ICU and p is the average timespent in ICU. Here  , where β is the ICU admission rate by infection. The γ coefficient iseasy to measure because it relates two quantities that are usually carefully monitored (number of deaths and number of occupied ICU beds). The relation (2.6) is therefore verifiable.
, where β is the ICU admission rate by infection. The γ coefficient iseasy to measure because it relates two quantities that are usually carefully monitored (number of deaths and number of occupied ICU beds). The relation (2.6) is therefore verifiable.
The relation (2.6) is easily extended to the number of occupied beds in hospital, replacing t by the time between infection and admission in hospital, p by the length of stay in hospital and replacing γ by a corresponding coefficient.
We will choose here to study the evolution of  rather than the evolution of An (although the latter is easy to deduct). Indeed,
rather than the evolution of An (although the latter is easy to deduct). Indeed,  is an important marker in practice.
is an important marker in practice.
The relations (2.5) and (2.6) can be used in (2.4) to infer similar decoupled models for the dynamics of In and An. In particular, the following infection-infection model is obtained
 (2.7)
(2.7)
This identity has two remarkable advantages. On the one hand, it does not involve the mortality rate. On the other hand, it focuses only on infection rate. Actually, by introducing the daily infection rate
![\[ i^{\star}_{n} = \frac{i_n}{P}, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq16.png)
identity (2.7) becomes
 (2.8)
(2.8)
This infection-infection model is moreover independent of the overall size of the population studied. It can be used when we have a few successive surveys measuring the infection rate. We will come back to that point in Section 6.2.
It remains to estimate the number of recovered cases. It is calculated by the relation
 (2.9)
(2.9)
where s is the average recovery time. The number of susceptible individuals can be easily deduced from the identity
 (2.10)
(2.10)
Identities (2.3), (2.5), (2.6) and (2.9) are sufficient to describe the evolution of the quantities Dn,  , In and Rn, provided that they are completed with initial data I0, ⋯, Im−1 (which is equivalent to Dr, ⋯, Dr+m−1). However, according to the formula (2.4) it is not necessary to go back to the initial conditions at the start of the epidemic, which are generally not well known. Mortality figures in the early stages of the epidemic can be used over a time interval of m + ℓ days. This provides a robustness of the model with respect to the initial conditions at the start of the epidemic.
, In and Rn, provided that they are completed with initial data I0, ⋯, Im−1 (which is equivalent to Dr, ⋯, Dr+m−1). However, according to the formula (2.4) it is not necessary to go back to the initial conditions at the start of the epidemic, which are generally not well known. Mortality figures in the early stages of the epidemic can be used over a time interval of m + ℓ days. This provides a robustness of the model with respect to the initial conditions at the start of the epidemic.
Remark 2.1.
The formula (2.6) can be used to predict mortality a few days before (8 days in France for example) from the number of occupied ICU beds (2.3). Actually, one can rewrite it in the form
Remark 2.2.
The above model can be completed by taking into account changes in overall population size. This is equivalent to considering population size as a sequence 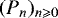 governed by a relation of the form
governed by a relation of the form
where τ = τ+ − τ− is the difference between the daily fertility rate τ+ and the non-epidemic all-cause mortality rate τ−. In this case, the number of susceptible individuals can be calculated by a recurrence formula of the type
 (2.13)
(2.13)
Then we can readjust the model (2.3). One can also integrate the fact that a part of the population is initially immunized as well as the re-infections of the same individuals in the longer term. These extensions will be the subject of a forthcoming work.
3 Calibration of model parameters
The model described in the previous section is essentially based on two families of parameters which will be set by calibration from the data: the clinical times inherent to the illness and the normalized coefficients of transmission λ0, ⋯, λℓ−1. There is also the coefficient γ linking the number of occupied ICU beds to mortality, as well as the infection fatality rate α (we will see that it has alimited impact on the mortality and on the occupancy of ICU). We are going to calibrate these parameters (with the exception of α) using on the one hand, clinical data available in the literature, and on the other hand, mortality data published daily. The aim is to make the model as close as possible to reality and to be able to make forecasts for the weeks and months ahead. Note that the daily reproduction number Cn is a dynamic parameter which will be the focus of specific discussions thereafter.
3.1 Determining clinical delays
Recent studies place the onset of Covid-19 between the 2nd and 14th day, with a median around 5 days (see, e.g., [27, 29, 33, 50]). However, it is now known that infected individuals can be contagious in the pre-symptomatic phase up to two days after infection (see [28, 49]). This is supported by estimates of the mean serial interval (the time interval between the illness onset of a person already infected and of a person subsequently infected). In [14], it is estimated to be 4 days. It is estimated to be 5.1 days in [50]. These are two of the main causes of rapid circulation of the Sars CoV-2 virus. The value m should therefore be set at 2 (remember that m is not the average time of onset of contagiousness nor the incubation period. It is a minimum time from which the infected individual becomes contagious).
In addition, a viral load may remain in the nasopharynx for up to 17 days (very exceptionally up to 21 days) after illness onset (see [28, 51]), suggesting a period of contagiousness of up to 17 days. We choose ℓ = 17.
The time from illness onset to hospital admission is usually 3 to 9 days (see [29, 50]). According to [51], arrival in ICU occurs on average within 12 days of onset. It is estimated to be 14.5 days in [33]. Again, taking into account the incubation period, we choose t = 19.
According to [29, 33], the average time of death is 17 to 24 days after the illness onset. Adding the average length of the incubation period, we choose r = 25 (average time between time of infection and death). The average time from infection to recovery is estimated at 22 days: s = 22 (see [43, 51]). Finally, the average length of stay in ICU (in France) will be chosen equal to 17 days (see [38]): p = 17.
3.2 Model transmission coefficients
In order to complete this set of parameters, the transmission coefficients λ0, ⋯, λℓ−1 still need to be fixed. We choose to set them by a least squares technique using mortality or in-hospital mortality data over a certain calibration period. It should be noted that the calibration period in question is chosen according to the country by meeting twocriteria. The first criterion is that the mortality figures should be fairly significant (i.e. not at the very beginning of the epidemic where the death figures are still not very representative). The second criterion is that the interventions applied to contain the epidemic are not variable during a part of this period. For the sake of simplicity, the mathematical explanation of this least-squares technique is given in Appendix A.2.
These coefficients have been estimated for several countries where the epidemic has advanced sufficiently or even strongly. For each country, a calibration period was chosen that met both of the above criteria. The resulting coefficients and calibration periods are detailed in Table A.1 (in the appendix). The fact that these coefficients are close to each other reinforces the idea that they are a characteristic of the epidemic. In addition, similar values of these coefficients are found worldwide. However, in the case of South Korea, the coefficients are significantly different. It is concluded that the strategy used by South Korea has had a direct impact on the distribution of transmission probabilities during the period of contagiousness.
3.3 The infection fatality rate (IFR)
The difficulty in finding reliable estimates of the infection fatality rate (IFR) is a surprising fact about this epidemic. In the urgency of the crisis, screenings are often restricted to individuals with severe symptoms. This is a non-random sample of the population. However, a screening campaign based on the same principle as surveys could lead to an estimate of this rate after a certain waiting period (as well as the infection rate at a given time).
Today, the first estimates available in the literature are often based on data in China [43] or concerning passengers of the Diamond Princess cruise ship [37]. In [37], it is estimated at 1.2% for Diamond Princess passengers and 0.6% for China. In the case of France, a similar estimate can be found in [38]. Nevertheless, these estimates are not the only ones, and it is not excluded that the rate is higher [12, 36, 47].
In the following, simulations will be based on the number of in-hospital deaths in France and for two values: α = 0.6% and for α = 1.2%. It follows that α is the infection in-hospital fatality rate and is slightly lower than the IFR.
3.4 The coefficient of proportionality γ
The coefficient γ links two important indicators through the identity (2.6): the number of deaths and the number of occupied ICU beds. Since reliable figures are available for these indicators (if we restrict ourselves to deaths in hospital), we would like to check first the validity of the proportionality identiy (2.6) which has not been deduced from the observations. For this purpose, we choose hospital fatality data and the number of people in ntensive care in France. These two figures are communicated on a daily basis by Santé Publique France since March 17th 2020. In the Figure 1 we visualize the evolution of the ratio
![\[ \gamma_n= \frac{A^{\star}_n} { D_{n+r-t} -D_{n+r-(t+p)}} \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq25.png)
from March 31 to April 13, 2020, according to in-hospital mortality data in France. The values of r and p chosen at the beginning of this section (r = 25, p = 17) have been adopted here. It can be observed that this ratio is almost constant, confirming the hypothesis of the model that led to this identity. In the following, we will choose the value γ = 0.94.
 |
Fig. 1 The ratio γn calculated from March 31st to April 24th 2020. It can be observed that this ratio is almost constant, confirming the assumed proportionality of the two quantities. |
4 Evolution of the daily reproduction number
The daily reproduction number Cn plays a prominent role in this model (Cn will act as a dynamic basic reproduction number). By keeping Cn below 1, the epidemic decreases until it is extinguished. The rigorous proof of a threshold theorem for this model, not really difficult, will be done in a future work (here we give a numerical proof). As for the basic reproduction number, formula (A.6) indicates that this number Cn is directly related to the average number of contacts of an infected person on day n, to the average transmission probabilities and to the duration of contagiousness. Its estimation from epidemic data allows to quantify the effectivenessof the interventions and to design realistic scenarios for the future.
For periods of time already passed, this parameter can be estimated by the formula (2.3) with a delay time of r days
 (4.1)
(4.1)
The time r reflects the fact that any change in the interventions (or in the behavior of the population) on day n will only have an impact on the number of deaths from day n + r. This delay in estimating this number can be overcome if accurate data are available on the rate of infection. Actually, one can use the formula without delay
 (4.2)
(4.2)
The usefulness of this second formula and its advantages will be discussed in Section 6.2. At the present stage, the delayed formula (4.1) is used to estimate Cn in the past.
The evolution of Cn has been reproduced for several countries and for the whole world. For China (Fig. 2), the most intense period of the epidemic is chosen, i.e. from mid-January to early March 2020.
In the case of France, Italy and Spain, Cn is shown in Figure 3 until April 5th 2020 (data sources are given at the end of the paper).
A closer look at the values obtained Cn for the totallockdown period in France, Italy or Spain shows that it is generally between a minimum value C− ≈ 0.6 and 1. The average for the strict lockdown period from March 17 to April 5, 2020 is 0.83 for France and Spain and 0.88 for Italy. It is not excluded that these averages slightly decrease if the strict lockdown lasts longer, especially because the individuals in contact remain the same. Indeed, if we observe this average for France over the period from April 1 to 7, 2020, it is declining and has reached 0.66.
The curve shows the different dates of entry into lockdown for the three countries.
Changes in Cn for a few other countries were calculated from public data (some public data sources are listed at the end of the paper). In Figure 4 the evolution of this daily reproduction number is shown for Belgium, Germany and South Korea. In Figure 5, this rate is evaluated for the United States and the United Kingdom. The effectiveness of the public interventions in South Korea can be clearly seen, since the daily reproduction number in this country is, in average, the lowest of all the countries illustrated here.
A first remark should be made at this stage: drastic restrictions of the strict lockdown lead to values of Cn barely lower than the threshold value 1. It can indeed be observed that outside a regime of drastic restrictions, values of Cn are clearly higher than 1, even in periods with strong but not drastic interventions. This observation suggests that it will be difficult to control the epidemic in the long term without the application of drastic interventions. Thus, according to these estimates, deconfinement, even moderate, will systematically make the value of Cn greater than 1. In the case of Covid-19, we are faced with a dilemma: to maintain a strict lockdown with numerous socio-economic and systemic damages or to proceed to a deconfinement not totally under control risking a rebound of the epidemic.
 |
Fig. 2 Evolution of the daily reproduction number for China for the period from January 23rd to March 3rd 2020 during the Coronavirus Sars-CoV-2 pandemic. This number is calculated from mortality data. |
 |
Fig. 3 Evolution of the daily reproduction number for France, Italy and Spain for the period from February 23rd to April 6th 2020 during the Coronavirus Sars-CoV-2 pandemic. This number is calculated from mortality data. |
 |
Fig. 4 Evolution of the daily reproduction number for Belgium, Germany and South Korea from February 28th to April 5th 2020 (Covid-19 pandemic). |
 |
Fig. 5 Evolution of the daily reproduction number for the period from the end of February to the beginning of April 2020 for the United States and the United Kingdom (Covid-19 pandemic). |
5 Scenarios for the evolution of the epidemic
We are now able to use the calibrated model for studying some future scenarios of the epidemic. Although the model is independentof the choice of country, we will focus on the French situation as an example of study. In general, the results obtained for other countries lead to similar conclusions, and can be easily replicated.
The study of these scenarios will be used in the design of a lockdown exit strategy.
Eleven scenarios, numbered from 0 to 10, are studied here. For all these scenarios, the focus will be on the evolution of five markers: the number of deaths in hospital, the number of occupied ICU beds, the number of active cases, the number of recovered cases and the number of infected individuals. Again, it should be noted that the estimates of the first two markersprovided by this model are little dependent on infection fatality rates, except when the epidemic is large1.
Scenario 0 relates to the evolution of the epidemic in the case where strict lockdown had not been imposed and the epidemic was allowed to run its course while strong but less drastic interventions were applied. This scenario will give us an accurate idea of the severity of this crisis and what was avoided.
Scenario 1 consists of extending the strict lockdown beyond May 11th (the French government has set this date to relax the lockdown).
The 2nd and the 3rd scenarios describe a moderate deconfinement installed abruptly by May 12, 2020, or achieved gradually (over about a month).
Scenarios 4 and 5 involve a switch to a cyclic situation of alternating strict lockdown and deconfinement, with periods of equal durations.
Scenarios 6, 7, 8, 9 and 10 involve alternating lockdown and deconfinement based on an organized schedule (e.g., lockdown on some but not all days of the week).
5.1 Scenario 0: evolution of the epidemic without lockdown
Prior to imposing lockdown on the population, almost all the nations have tried to block the introduction of the virus into the country, without any real success. They then tried to curb its circulation. If we look again at the curves of the daily reproduction number, we can see that interventions in the pre-lockdown period have contributed to a serious drop in this number, but rarely below 1. In France, in the ten days prior to entry into strict confinement, Cn had an average of 1.4. That is way lower than the values prior to this period, but this rate remains far enough away from the 1 threshold value.
In this scenario 0, we want to measure the impact of the strict lockdown, imagining that it had not been imposed, but keeping some strong interventions. It is therefore not the scenario where nothing is done (which will be much more catastrophic) but the scenario where the interventions are not sufficient. We will impose here a value of Cn equal to 1.3, and this will be effective from March 17, 2020, while keeping the actual data before that date. Note that in France, Italy and Spain, and in many other countries, this value of 1.3 is lower than the mean value measured the week before the lockdown (see Fig. 3).
In Table 1, we indicate some figures from the simulations within the framework of this scenario. The evolution of the five markers chosen for these simulations is the subject of Figures 6 and 7.
The results confirm that strict lockdown has prevented a much more severe health situation than the one currently experienced.Indeed, under the conditions of rather strong interventions of this scenario, and with a fatality rate α =0.6%, 100.000 deaths would have occurred in France in mid-June, and almost 170000 at the end of August. The needed ICU beds would have exceeded 10000 places (per day) on April 14th 2020, and 28000 places at the end of May 2020. The epidemic would have continued togrow until it peaked in the last week of May 2020. On August 31st 2020, the number of infected people will reach, according tothis scenario, a little over 29 million (43.2% of the French population). It is noted that with a reproduction rate of 1.3, the epidemic reached its peak after a delay of 2.5 to 3 months after March 17th. With a higher reproduction rate, this period is obviously shortened.
An important conclusion which is necessary at this stage is not only to confirm the effectiveness of strict lockdown, but to note that the coronavirus Sars-CoV-2 leaves an extremely narrow margin of maneuver to control its circulation (let us recall indeed that this scenario 0 is that of the continuation since March 17th of strong but not drastic interventions). This observation will be reinforced when scenarios with even stronger interventions are analyzed.
It is nevertheless useful to indicate that according to this model, strict lockdown has saved France about 1233 in-hospital deaths as ofApril 15th 2020, and about 7496 hospital deaths as of April 27th 2020 (i.e. 12 days later). We will see thereafter (scenario 1) that this reduction in the number of deaths due to lockdown will be around 21720 cases on May 11th, and around 80928 cases on June 15th 2020. It has also avoided an overflow of the hospital system that would have occurred as early as mid-April (see Tab. 1 and Fig. 7).
 |
Fig. 6 Scenario 0 in France. Left: total number of deaths in hospital. Right: daily deaths in hospital. Values up to March 17th 2020 are actual (public data). |
Scenario 0 (evolution of the epidemic in France without strict lockdown on March 17th 2020). Main indicators on the date of relaxing lockdown (May 11th), June 15th, July 31st and August 31st 2020.
 |
Fig. 7 Scenario 0 in France. Left: number of occupied ICU beds (estimated by the model). Right: evolution of the number of active cases, the number of infected individuals and the number of recoveries until early December 2020 (estimated by the model). We observe that the peak of the epidemic occurs at the beginning or end of June 2020, depending on the value of the IFR. Values up to March 17th 2020 are actual (public data). |
5.2 Scenario 1: continuation of strict lockdown
Here we would like to study the consequences of the eventuality (now ruled out) of an extension of the strict lockdown in France after May 11th 2020, with the same interventions. To do so, we set Cn = Cconf after this date, with Cconf = 0.83 (which is, itshould be remembered, close to the average value observed in France, Spain and Italy during strict lockdown).
We ran simulations with two values of α: α = 0.6% and α = 1.2%. We found that the predicted number of hospital deaths and ICU needs are almost the same for both values, in accordance with the observations made previously (if the epidemic is not significant in terms of the number of infected people, the IFR has little influence on the model’s predictions of mortality and ICU needs).
In Table 2, some numbers predicted by the model have been given. Figures 8–9 summarize the evolution of different indicators when strict lockdown is maintained.
In comparison with scenario 0, we observe that at May 11th 2020, the model predicts that lockdown will save approximately 21720 lifes. The number of deaths per day will be about 165 (compared to 175 on March 17th 2020). About 2,668 places in ICU will remain occupied. However, it should not be concluded that strict lockdown only postponed a situation by two months. It is indeed necessary to take into account delays between infection and admission to resuscitation or death.
On the other hand, the model predicts a number of active cases on 11/5/2017 equal to 386,335 cases. To find an equivalent number of active cases, the model indicates that it is necessary to go back to March 3rd 2020 i.e. two weeks before lockdown (see Fig. 9). At 17/3/2020 (start of strict lockdown), the number of active cases is estimated at 1,415,775 cases. In terms of the number of active cases, on 11/5/2020, when strict lockdown is due to end, the situation in France will be similar to that of March 3rd 2020 (in almost two months, strict lockdown has reduced the number of active cases by a dozen days).
If strict lockdown is extended beyond May 11th, the simulation predicts that the number of deaths per day and the number of occupied ICU beds will drop significantly before the end of June (see Table 2). By the end of July, the total number of hospital deaths will be approximately 22,240 if α = 0.6% and about 23,025 if α = 1.2%. It will only increase very slowly thereafter.
Scenario 1 (continuation of lockdown in France after May 11th 2020). Main indicators at the date of relaxing lockdown (11/5/2020), June 15th, July 31st and August 31st 2020.
 |
Fig. 8 Scenario 1 in France. Left: total number of deaths in hospital. Right: daily deaths in hospital. Values up to April 30th 2020 are actual (public data). |
 |
Fig. 9 Scenario 1 in France. Left: number of occupied ICU beds (estimated by the model). Right: number of active cases, of the number of infected persons and of recovered persons until December 4th 2020 (estimated by the model). Values up to April 30th 2020 are real (public data). |
5.3 Scenarios 2 and 3: direct or progressive moderate deconfinement
The estimation of the daily reproduction number, discussed in Section 4, revealed that a progressive deconfinement leading to values of Cn lower than 1 will be difficult to achieve, unless new drastic interventions replace strict lockdown.
Scenarios 2 and 3 look at a lifting of strict lockdown in two ways. The first way (scenario 2) is to move directly to a soft deconfinement by lifting the lockdown abruptly on May 12th 2020. By “soft deconfinement" we mean a slightly relaxed lockdown or a partial lockdown (that is, a situation with strong interventions that are not totally drastic). The second way will be to reach the same deconfined regime in a “gradual" manner, i.e. after a transition phase of one month (from May 12th to June 15th 2020). On arrival (i.e. in deconfinement regime), a daily reproduction number slightly higher than 1 will be imposed.
In the results presented here, we choose Cn = 1.2 in deconfinement period (starting May 12th in scenario 2, and reached linearly on June 15th in scenario 3). This value is not very far from that obtained by lockdown. In particular, it is significantly lower than the mean value observed in France the week before the strict lockdown (it was around 1.40, when some interventions to curb the transmission of the virus were already in place). In other words, these two scenarios 2 and 3 are almost minimalist (i.e. without exaggerating the consequences of deconfinement). In both the scenarios, we set Cn = Cconf = 0.83 between May 1st and May 11th (the deconfinement date). The data before April 30th are actual.
We impose an infection in-hospital fatality rate α = 0.6%.
The results of the simulations are described in Figures 10, 11 and 12. In both cases, the epidemic is again on the rise, with a time lag of one and a half months between the two scenarios, and a slight reduction in the magnitude of the epidemic in the event of a gradual deconfinement. In both scenarios, the peak of the epidemic will be in the period from mid-October 2020 to the end of November 2020, i.e. next fall, i.e. between four and a half and five and a half months after the start of deconfinement.
In addition, according to the model, the number of ICU beds required will exceed 5,000 by the end of August 2020 for Scenario 2, and by mid-October for Scenario 3. As of August 31st, 2020, the infection rate of the population will be about 12.15% for scenario 2, and 8.67% for scenario 3. These two rates will reach 27.35% and 25.22% by March 1st 2021. In both scenarios, the total number of deaths exceeds 95,000 by the end of February 2021.
In conclusion, a scenario of measured deconfinement, whether sudden or gradual, will not be effective in the mid- or long-term even with strong interventions (i.e. slightly less stringent than those of strict lockdown). Such deconfinement will only push the peak of the epidemic into the last quarter of the year.
 |
Fig. 10 Deconfinement Scenarios 2 and 3 (France). Left: total number of deaths in hospital. Right: daily deaths in hospital. Scenario 1 of continuation of strict lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
 |
Fig. 11 Deconfinement Scenarios 2 and 3 (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
 |
Fig. 12 Deconfinement Scenarios 2 and 3 (France). Total number of infected individuals until early March 2021. |
5.4 Scenarios 4 and 5: periodic (or cyclic) deconfinement
We are now studying original scenarios consisting of alternating two phases: a phase 1 of strict lockdown with drastic restrictions, and a phase 2 of moderate deconfinement with slightly less drastic restrictions. It will be assumed that the two phases have the same time duration T∕2 (alternating with unequal durations will be discussed in the following scenarios). We impose a daily reproduction number Cn = Cconf in the phase of strict lockdown with Cconf = 0.83. In the soft deconfinement phase, a value Cdeconf is imposed, with Cdeconf = 1.1 (4th scenario) or Cdeconf = 1.35 (5th scenario). Qualitatively a value of Cdeconf close to 1 means that the deconfinement practiced in phase 2 is accompanied by strong interventions to curb the circulation of the virus. A periodicity of T = 2 days is adopted (i.e. strict lockdown every other day). Note that this periodicity does not have much influence on the obtained results (we obtain practically the same results with alternating every other week). We choose to run simulations with a fatality rate α =0.6%. The simulations with other values of α give qualitatively similar results, but with numbers that may differ.
We are mainly interested in the influence of the daily reproduction number practiced on the days of deconfinement Cdeconf.
In Figures 13 and 14, the evolution of the main indicators of the evolution of the epidemic was visualized with a periodicity of one day. The curve of active cases (Fig. 14) shows that scenario 4 leads to the extinction of the epidemic, a little slower than strict lockdown. The cumulative number of in-hospital deaths will reach about 25074 on August 31st, and 27900 in early March 2021 (compared to 24600 with continuation of the strict lockdown). By the latter date, the percentage of the population having been infected will be 6.96%. It is therefore not a scenario of herd immunity.
As for scenario 5, the epidemic is curbed but not stabilized. The epidemic rises slowly and then falls back, over several months. The peak is reached about 4 months after the start of deconfinement. The number of in-hospital deaths will fluctuate between 70 and 160 until February 2021. Similarly, between 1500 and 2300 ICU beds will remain occupied until February 2021. In the long term, the cumulative number of in-hospital deaths will reach around 29800 by the end of August and continue to rise to 50200 by the beginning of March 2021. By the latter date, 12.92% of the French population will have been infected. This scenario is not that of a herd immunity.
Naturally, if we choose a value of Cdeconf greater than that adopted in this scenario 5 (where Cdeconf = 1.35), the epidemic will become even more widespread. Unsurprisingly, an alternation of strict lockdown - total deconfinement is to be excluded.
We conjecture at this point that the extinction condition of the epidemic in this scenario is written as follows
 (5.1)
(5.1)
where Cmean is a mean value of Cconf and Cdeconf. The search for the exact expression of this mean value is a mathematical question that we do not address in this work. However, we can make the approximation that Cmean is close to the arithmetic mean of Cconf and Cdeconf (the durations of the two phases being equal). This results in the following approximate criterion for a periodic-type scenario to stabilize or mitigate the epidemic without amplifying it:
![\[ \frac{{C_{\textrm{conf}}}+{{C}_{\textrm{deconf}}}}{2} \leqslant 1, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq29.png)
We saw in paragraph 4 that in several countries (including France) the lockdown leads to values Cn in general around 0.80. If we use this value as a reference we deduce the following constraint on Cdeconf:
 (5.3)
(5.3)
This approximate criterion is used here, although it is not exact. It defines the level of periodic deconfinement compatible with the control or extinction of the epidemic. We will come back to this point during the so-called zigzag strategy.
 |
Fig. 13 Scenarios 4 and 5 of periodic deconfinement (France). Left: total number of deaths in hospital. Right: daily deaths in hospital. Scenario 1 of continuation of strict lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
 |
Fig. 14 Scenarios 4 and 5 of periodic deconfinement (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
5.5 Scenarios 6 to 10: scheduled deconfinement
In this last series of simulations, we imagine epidemic control scenarios based on a precise schedule of strict lockdown on certain days of the week (or of the month) and soft deconfinement on the other days. We will call it a scenario of weekly organized deconfinement. One can also adopt a monthly organized deconfinement, choosing certain days of the month for strict lockdown.
More generally, such a scenario can be imagined by organizing a duration W (W = 7 when it is a weekly scenario), which will then be repeated identically.
Let k, 0 ≤ k ≤ W, the number of days of deconfinement over that period. Note again Cdeconf the daily reproduction rate during these deconfinement days. The remaining W − k days are days of lockdown. One of the questions that occurs naturally is how many days per week at most can be relaxed (i.e. softly deconfined) without a resumption of the epidemic?
For simulations, we choose W = 7 (week). We impose on the days of strict lockdown Cn = Cconf = 0.83 (average value observed during strict lockdown in France). The days of deconfinement (or relaxed lockdown) we impose a rate Cdeconf = 1.35 > 1. The same value of α =0.6% is maintained in these simulations (simulations carried out with other values give qualitatively similar results). The scenarios studied correspond to k = 5 deconfinement days per week and W − k = 2 lockdown days (scenario 6), k = 4 (scenario 7), k = 3 (scenario 8), k = 2 (scenario 9) and k = 1 (scenario 10).
The evolution of the different indicators is illustrated in Figures 16, 17 and 18. It can be observed that for 1, 2 or 3 days of deconfinement per week (scenarios 8, 9 and 10 respectively), the epidemic continues to die down at various speeds. On the other hand, when deconfinement occurs 4 or more days per week, the epidemic starts to rise again with apeak reached on mid-October 2020. On March 5th 2021, with 5 days of deconfinement, the model predicts that at least 27.3% of the French population will be infected, compared to 16.75% for 4 days, 9.43% for 3 days of deconfinement, 6.74% for 2 days and 5.90% for one day. So these are not gregarious immunity scenarios.
Based on these simulations, it remains to be determined how many days of strict lockdown within a week are necessary to control the outbreak (we want to define a simple rule). Of course, this number depends on the quality of the deconfinement, i.e. the level of restrictions applied on deconfinement days. As in the previous section, it is assumed that it boils down to a condition of form (5.1) with Cmean an average daily rate expressed as a function of Cconf and Cdeconf. Here we will approximate it by th arithmetic mean of Cconf and Cdeconf weighted by number of days in every regime. We get the approximate condition
![\[ \frac{ ({W}-k){C_{\textrm{conf}}} + k {{C}_{\textrm{deconf}}}}{{W}} \leqslant 1, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq32.png)
It can be observed that this upper limit k+ of the number of deconfined days is naturally decreasing with respect to Cconf and Cdeconf respectively. A deconfinement at least one day per week is possible if
![\[ {W} \frac{1-{C_{\textrm{conf}}}}{{{C}_{\textrm{deconf}}}-{C_{\textrm{conf}}}} \geqslant 1. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq34.png)
This conditions means that
 (5.5)
(5.5)
In the case of a weekly organized deconfinement and with choice Cdeconf = 0.83, the constraint (5.4) is written
 (5.6)
(5.6)
where Cdeconf indicates the level of interventions during deconfinement. In this case C⋆ = 7 − 6Cconf ≈ 2.02. Note that this limit is independent of the fatality rate by infection.
Thus, in conclusion, an organized weekly deconfinement makes it possible to stabilize the epidemic under two conditions
- (i)
a deconfinement level not exceeding the C⋆ bar,
- (ii)
a number of deconfinement days per week checking the constraint (5.6).
As an example, if we want a deconfinement level comparable to that of the week preceding the decision of lockdown in France, the constraint (5.6) gives k ≤ 2.08, where we used the value Cdeconf = 1.40 (mean value observed the week preceding the decision of strict lockdown in France. See Sect. 4). In other words, a deconfinement of 3 days (or more than) per week with interventions comparable to those applied the week before the lockdown in France does not guarantee an extinction or stabilization of the epidemic.
 |
Fig. 15 Scenarios 4 and 5 of periodic deconfinement (France). Total number of infected individuals until early March 2021. |
 |
Fig. 16 Scenarios 6 to 10: weekly organized deconfinement (France). Left: total (cumulative) number of deaths in hospital. Right: deaths in hospital. Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
 |
Fig. 17 Scenarios 6 to 10: weekly organized deconfinement (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
 |
Fig. 18 Scenarios 6 to 10: weekly organized deconfinement (France). Total number of infected individuals until early March 2021. |
6 A zigzag strategy to control the epidemic
6.1 Schemes and principles of the strategy
We propose here a non-pharmaceutical strategy to get out of the strict lockdown, while stabilizing or gradually reducing the outbreak. To explain this strategy, we need to classify the regime of restrictions into four lanes2 defined as follows and represented in Figure 19. Let us add that this classification and the resulting strategy are by no means a view of the mind. They stem directly from the detailed study in parts 4 and 5 (see, for example, Fig. 20 where the daily reproduction number for France, Spain and Italy, is reproduced with the limits of the four lanes).
-
The first lane is the drastic lane. This is the situation that results from a regime of drastic restrictions (at least equivalent to strict lockdown). Mathematically, this means that Cn ≤ 1. In practice, strict lockdown in France, Italy and Spain indicate that this number is generally between C− = 0.6 and 1 with an average of approximately 0.83. This is therefore a narrow lane.
-
The second lane is the semidrastic lane. It is characterized by a slight relaxation of the drastic interventions or by a set of stronginterventions not reaching in balance those of a drastic regime. Mathematically, it is characterized here by a daily reproduction number Cn satisfying 1 < Cn ≤ C+ ≈ 1.2. It is alsoa very narrow lane. We will see that this lane will play an important role in the deconfinement strategy we are proposing.
-
The third lane is the intermediate lane (or cautionary lane). It is characterized by a situation in which the population is alerted of the presence of the virus and adopts precautionary measures and behaviors that are objectively insufficient to limit its circulation. At this stage, public interventions aim to curb the epidemic, without necessarily being restrictive (restaurants, coffee shops, schools, public establishments and public transport are still open). Mathematically, it is characterized by a daily reproduction number satisfying C+ ≤ Cn ≤ C⋆, with C⋆ ≈ 2.
-
The fourth lane is the relaxed lane (or carefree lane). It is characterized by the total or almost total absence of restrictions. It corresponds to the situation of ordinary and unrestricted lifestyle, either because the virus is not present in the population, or because it is still in the introduction stage and that the population is reckless. Mathematically, this lane is characterized by the condition Cn ≥ C⋆.
Let us make some observations:
-
Switching from one lane to another is done by adding or relaxing interventions. In view of the data, we conjecture here that these interventions are of the order of those indicated on Figure 19.
-
only thedrastic lane leads to an extinction of the epidemic. The other three lanes are conducive to its spread, but at different rates. Thus, any strategy of deconfinement that excludes the drastic lane will lead to a rebound in the epidemic in the short to medium term.
-
the relaxed lane is a lane to be excluded in any deconfinement strategy (in the absence of drug solutions). Indeed, it is a way without interventions and is very conducive to contagion. It should not be used in the presence of the virus (even for one day per week).
These observations explain the dilemma faced by almost every country in the world: in the absence of pharmaceutical solutions, the narrow and very expensive lane of drastic interventions must be taken.
As it stands, the reasonable time frame for quantifying the impact of any measure on deaths is approximately 25 days to 1 month. It is also a delay that allows to measure retroactively the daily reproduction number and and to determine which lane has been taken. However, a practice of mass screening can considerably shorten this time frame and lead to a real-time conduct of the interventions. We will come back to this point later.
In light of the analysis of different exit scenarios studied in Section 5, a gradual zigzag strategy for exiting lockdown while controlling the epidemic is proposed here. This strategy is based on a weekly organized deconfinement that can be adjusted over time (as a reminder, weekly organized deconfinement consists of imposing strict lockdown on certain days of the week, and moderate deconfinement on the other days).
This strategy, called zigzag strategy, has several phases
-
The first phase consists of a weekly organized deconfinement with a maximum of 2 deconfinement days per week. Deconfinement on these two days must be accompanied by strong interventions limiting the circulation of the virus (the effect of which will be measured in the next step). If we take the classification below, this amounts to changing the lane two days a week, as illustrated in Figure 21 andreturning to the drastic lane on the other days (hence the name zigzag strategy). Such deconfinement can tolerate the use of part of the intermediate lane when the number of days of deconfinement is equal or less than 3 days. This lane becomes prohibited when the number of days of deconfinement is greater than 3.
-
The transition from one phase to the next is made after measuring the impact of deconfinement by estimating the daily reproduction number from the main indicators using the formula (4.1), or possibly the formula (4.2). From this, we deduce Cdeconf during the days of deconfinement. The number of deconfinement days is then decided in the next phase according to the simplified rule (see Sect. 5.5):
![\[ \mbox{ Number of days of deconfinement per week $\displaystyle{\leqslant {W}\frac{1-{C_{\textrm{conf}}}}{{{C}_{\textrm{deconf}}}-{C_{\textrm{conf}}}}}$.} \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq37.png)
The number of deconfinement days may increase, remain the same, or decrease. It decreases if it is found that deconfinement has has not been sufficiently moderate.
This strategy remains flexible. For example, we can adopt a deconfinement at scheduled months, with exactly the same phases, but by replacing the above rule by the rule (5.4) with D = 30.
Similarly, if Cdeconf is below 1.2, we can also adopt a periodic deconfinement: we alternate periods of strict lockdown and deconfinement with equal durations (see Fig. 22). Periodic deconfinement has been discussed in Section 5.4. It is illustrated in the diagram in Figure 22.
Periodic deconfinement uses only two lanes: the drastic lane and the semi-drastic lane. It has the advantage of allowing a free choice of the length of the period, as it does not have much influence on the results obtained. One can thus opt for every other confined day, or every other confined week, etc. Nevertheless, the period should remain small compared to the time needed to reach the peak of the epidemic if deconfinement is maintained (which is in the order of 4 to 5 months). Qualitatively, a periodic deconfinement is equivalent to a weekly organized deconfinement with 3 and a half days of strict lockdown per week. Therefore, its success as a first phase of deconfinement cannot be guaranteed. Nor is it intended to be definitive (the goal being to deconfine completely). It is therefore a solution that can be adopted in the intermediate stages of the above zigzag strategy.
It should be noted that this zigzag strategy does not lead to herd immunity (on the horizon, the infection rate remains relatively low). It is therefore not an attenuation strategy like the one studied in [16]. Nor is it based on controlling the epidemic by using thresholds in the number of ICU occupied beds to trigger measures, as is the case with the suppression strategies proposed in the same paper [16]. Indeed, this zigzag strategy is based on an alternation between semi-drastic attenuation measures and suppression measures. It aims to control the total number of deaths in the long term (which automatically induces a control of the number of ICI occupied beds, according to (2.6)). Moreover, the fact that it is not very dependent on triggers makes it easier to program it in the medium or long term, while still being able to adjust it (by increasing or decreasing the number of deconfined days). Finally, the zigzag strategy can be used on a local, regional or national scale (with possible variations from one region to another). However, a local use, with a zigzag strategy by location or by region, seems to us to be the most effective, since it allows for regional heterogeneities to be taken into account.
 |
Fig. 19 Simplified four-lanes diagram showing the levels of interventions to curb the epidemic. |
 |
Fig. 20 Superposition of the limits of the four lanes with the evolution of the daily reproduction number for France, Italy and Spain (for the period from February 23rd to April 2nd 2020 during the Coronavirus Sars-Cov-2 pandemic) |
6.2 Usefulness of the generalization of screening tests
One of the greatest challenges in the fight against the Sars-CoV-2 Coronavirus pandemic is the estimation of the number of infected cases. The vast majority of these cases develop mild symptoms or are asymptomatic, requiring no hospitalization.
Today, the possibility of mass screening is becoming possible in many countries. In general, tests aim to detect the virus (virological tests) or to detect the presence of antibodies (serological tests). Many questions are raised regarding the use of these tests: privacy issues (in the case of mass tracking), respect for equality between individuals (if only immunized persons are allowed to go to work by issuing a so-called immunological passport), duration of immunity, etc. Moreover, the reliability and accuracy of these tests is itself subject to serious controversy.
Within the framework of the model proposed here and the zigzag strategy screening tests could have a decisive impact on how to manage the pandemics. Indeed, the adjustment of the zigzag strategy at the end of each of the above phases is based on the estimate of the daily reproduction number, which is considered here as the thermometer of the general situation. However, the estimation of this rate must be based on statistically reliable data. The use of fatality figures needs a period of 25 days, due to the delay between interventions and their effects on mortality. This could be slightly shortened by using ICU or hospitalization figures according tothe same model.
However, screening tests performed daily on a fairly representative sample in the manner of a survey can be used to infer the percentage of infected individuals in the population. In this case, it becomes possible to switch to a formula for calculating the daily reproduction number based on the infection rate of the population, and not on the number of deaths. Recall that according to (4.2), this formula is written as follows
![\[ C_{n} = \frac{i^{\star}_{n}}{\displaystyle{(1- \sum_{k=0}^{n-1} i^{\star}_k) } \displaystyle{\sum_{k=0}^{\ell-1} \lambda_{k} i^{\star}_{n-m-k} }}. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq38.png)
Unlike (4.1), this formula does not include the r delay time.
Such a breakthrough would put the finishing touches to the strategy to make it a real-time decision-making tool. By measuring the daily reproduction number on a daily basis, we can determine exactly what lane we are on, and therefore adjust the driving of the epidemic, without waiting for hospitalization or death figures.
7 Conclusions
The deterministic model introduced in this study is used to predict the dynamics Covid-19 epidemic and its impact on deaths and ICU occupancy. By relying heavily on public data, the model reveals several characteristics of the epidemic and inspires a plan to contain or stabilize it without resorting to herd immunity or strict long-term lockdown.
In the light of this model, it has been shown that moderate deconfinement with strong but non drastic interventions, whether gradual or sudden, can lead to a rapid resumption of the epidemic, with saturation of intensive care units in the fall and a peak of the epidemic in winter.
It has also been shown through this model that scenarios alternating strict lockdown and moderate deconfinement can allow the epidemic to be brought under control without resorting to group immunity. The weekly organized deconfinement scenario with some days of strict lockdown and other days of moderate deconfinement allows to curb the epidemic. Similarly, alternating strict lockdown - deconfinement in equal periods of time allows the epidemic to be controlled, provided that deconfinement contains some strong interventions. In the latter scenario, the choice of the length of the alternating period remains free and does not affect this finding. Let us add that in both scenarios, the number of infected individuals remains far from that of herd immunity and does not exceed 10% of the population.
Another finding of this study is that drastic interventions (like strict lockdown) are barely sufficient to control the epidemic. There is very little room for manoeuvre to alleviate these drastic interventions while controlling the epidemic.
In other words, any lockdown exit strategy must include not only strong interventions but also a calculated dose of drastic interventions (here, drastic interventions are defined as a set of interventions whose effectiveness when they are in effect is equal to or greater than that of strict lockdown).
Finally, the model and the simulations carried out made it possible to classify interventions into four lanes, one of which, the first, is necessary in any non-pharmaceutical deconfinement strategy (the drastic lane). The fourth lane is, on the contrary, to be excluded in any approach to controlling the epidemic. These lanes are schematized in Figure 19.
The result of all these elements is the gradual zigzag strategy that can control the epidemic by deconfinement, without exceeding 10% of infection in the population. This strategy consists in alternating days of strict lockdown and days of deconfinement according to a precise schedule calculated in advance and dynamically readjustable. This alternation can be organised by week, month or by any other period other period. In its intermediate stage, it can be periodic, with every other day of lockdown, or every other week, etc.
Schematically, this strategy consists in zigzagging between the different lanes mentioned above (see Figs. 21 and 22). It can be applied at local, regional, or national scales, without being invasive (as it does not require the use of personal data). This strategy is easily adaptable in the case of France, where the number of ICU occupied beds is an important factor in decision-making. Nevertheless, since the epidemic in France shows strong regional disparities, it could rather be applied at the local level.
It should be noted that regular surveys to measure the infection rate could greatly enhance this strategy by giving it real-time flexibility. It should also be noted that the model introduced here is based on average quantities and makes no distinction between infected persons who are detected and those who are not (only mortality plays an important role). This distinction is beyond the scope of this paper. Similarly, age is a risk factor influencing hospitalization and death figures and, consequently, the behaviour of individuals. Age structuring of the model and integration of confirmed and unreported cases will be the subject of a future work.
Finally, it should be pointed out that in the case of France, this model reveals that when the strict lockdown is lifted, scheduled for May 11th 2020, the situation will be comparable in terms of the number of active cases to that of March 3rd 2020. By this date, according to scenario 0, strict lockdown will have saved France around 21,700 deaths. The continuation of strict lockdown will lead to a significant drop in the number of deaths and the number of beds occupied in intensive care before the end of June. At the end of the summer, if strict lockdown is maintained, the number of deaths in hospital will be between 22240 and 23025 (depending on the IFR value). The study also revealed that if average interventions had been applied instead of strict lockdown (after March 17th 2020), the number of ICU beds required would have been around 30,000 at the beginning of June. By mid-June, the number of deaths in hospital in this case would be around 100,000.
 |
Fig. 21 Simplified diagram of a zigzag strategy by a weekly organized deconfinement. Here we have chosen Monday and Thursday as days of deconfinement. The other days of the week are lockdown days. Schematically, deconfinement amounts to a changeof lane, which can go up to the intermediate lane (because only two days per week are deconfined). The relaxed lane is excluded (or forbidden). When the number of days of deconfinement increases, the intermediate lane may become excluded as well. |
 |
Fig. 22 Simplified diagram of a zigzag strategy by periodic deconfinement. Strict lockdown and moderate deconfinement alternate over equal periods of time. Schematically, deconfinement amounts to a change of lane. The intermediate lane and the relaxed lane are prohibited in this strategy. |
Appendix
A.1 Formal justification of the model
The purpose of this annex is to set out the main ideas that led to the above model. It can be based on two very simple observations. The first is that at the time of a Covid 19 type crisis, most epidemiological data are communicated on a daily basis. The second observation is that, in general, particular attention is paid to the mortality figures caused by the epidemic. This is a universal marker in all countries of the world, often measured accurately (unlike the number of infected people, which is more difficult to quantify). It is therefore natural to consider a discrete model with the unit of time as the day, and which takes into account the evolution of mortality (and not only the number of infected persons).
We use notations introduced in Section 2.
Suppose an infected individual becomes contagious a few days after becoming infected and remains contagious for ℓ successive days. Thus, an individual infected on day Jk becomes contagious from day Jk+m and will remain so, at most, until day Jk+m+ℓ−1. It will cease to be contagious from day Jk+m+ℓ. If we now assume that this infected individual is in contact with N susceptible (or healthy) individuals during these days of contagiousness, we can assume that he will infect p0 N persons on the first day, p1N on the second to pℓ−1N on the last day, where p0, ⋯, pℓ−1 are probabilities of transmission of the disease.
In the absence of isolation measures, these pi parameters depend on the evolution of the viral load during the period of contagiousness; they are not necessarily equal. We will not fix thesecoefficients in advance. It is preferable to estimate them from actual data. Note, however, that they can be subject to additional constraints. We will come back to the profile of the parameters during their calculation, in Appendix A.2.
Note θn−1 the proportion of susceptible (uninfected) individuals at the end of the (n − 1)-day:
 (A.1)
(A.1)
where P − Dn−1 is the population size after the (n − 1)-day. Using the identity
![\[ S_{n-1} + I_{n-1} = P, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq40.png)
where we used the fact that Dn−1 remains small with respect to P.
Now, letus denote by χn the average number of people (susceptible or not) with whom an infected individual has contaminating contact the n day Jn, n ≥1. We may observe that only θnχn part is susceptible, and therefore can be infected by this individual.
We will now count the number in of individuals infected on day n. On that day, the contagious individual are those who are infected on days k where k satisfies
![\[ k+m \leqslant n <k+m+\ell, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq42.png)
that is n − (m + ℓ) < k ≤ n − m. Thus,
![\[ i_{n} = \sum_{k=n+1-(\ell+m)}^{n-m} p_{n-m-k} \theta_{n-1} \chi_n i_k, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq43.png)
where χn is the average number of individuals encountered by an infected individual on the nth day. We can write
![\[ i_{n} = \chi_n \frac{P- I_{n-1}}{P} \sum_{k=n+1-(\ell+m)}^{n-m} p_{n-m-k} i_k \mbox{ for } n \geqslant m. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq44.png)
We call the daily reproduction number on the n-th day the nonnegative parameter
 (A.6)
(A.6)
This parameter Cn is proportional to the average number of people who had contagious contact with an infected individual on the nth day, the duration of the contagiousness period and the average probability of transmission (this is similar to the law governing the basic reproduction rate R0). This coefficient Cn is a marker of the interventions in effect.
If we now go back to the model of the evolution of the size of the infected population in we can rewrite the equation (A.3) as follows:
 (A.7)
(A.7)
We now look at the evolution of the number of deaths. Here, we will assume that this number responds to a fundamental hypothesis for the following: the number of deaths caused by the epidemic before the nth day Jn is (uniformly) proportional to the number of individuals infected before (n − r)day, where r is is the average life span of an individual who died between the time of infection and death. This assumption will be considered true regardless of how this death figure is established (this number may represent in-hospital deaths). From a mathematical point of view, it means that there is a real α > 0 factor such that
 (A.8)
(A.8)
Combining with (A.10) we deduce the following model
 (A.10)
(A.10)
This model aims to describe the evolution of mortality due to the spread of a Covid-19 type epidemic, provided that the coefficients λ0, ⋯, λk are available. In the relation (A.4), we see that these coefficients are related to the parameters (or probabilities) of contagiousness p0, ⋯, pk that we could suppose to depend on the viral load of the individual during his period of contagiousness.
We do not have a priori a measure of these data. Nevertheless, we choose here not to make any hypothesis to impose values of them, but to use an inverse least squares method to calibrate them with fatality data. The objective is obviously to make this model as close as possible to reality.
When the size of the population is large, it can be considered that in the early stages of the epidemic, the number of infected individuals remains small with respect to the size of the population and one can write
![\[ I_n \ll P, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq53.png)
One can thus approach at the beginning of the epidemic the model above by the simplified linearized mode
 (A.11)
(A.11)
This linear model can be used in the early stages of the epidemic, when the number of infected individuals is still small relative to the size of the population.
Let us now estime the number recoveries. Note s the average recovery time. It can be estimated at 22 days (see, e.g., [43, 51]). Thus the number of individuals healed after the nth day is
![\[ R_n = I_{n-s} - D_{n-s+r} = (\frac{1}{\alpha}-1) D_{n+r-s}. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq56.png)
We are now looking at the number of people in intensive care units. The number of people admitted on n-day is an = An − An−1. If we consider that on average an individual having developed a severe form of Covid-19 stays p days in ICU, we can deduce that at the end of n-day, the number of individuals in ICU varied from an − an−p. Thus, at the end of the n-day the number of individuals in ICU is
![\[ A^{\star}_n = A^{\star}_{n-1} + (a_n -a_{n-p}). \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq57.png)
A.2 Identification of transmission coefficients by a least squares method
Here we explain the least-squares technique used to identify the transmission coefficients (λ0, ⋯, λℓ−1).
So let us assume that we have the fatality figures within a time window of K + (ℓ + m)+1 days {JL+2−(ℓ+m), ⋯, JL+K}, where K ≥ 1 is fixed.
In practice, this window is chosen so that the mortality figures are significant, i.e. not in the days when the epidemic begins to claim the first victims. Furthermore, it will be assumed that over the sub-window of time {JL+1, ⋯, JL+K} the interventions to contain the epidemic have varied little, i.e. the daily reproduction number remains essentially constant over this small period equal to an unknown C value. In the Table A.1 below in the appendix, the selected window was indicated for some countries. The coefficients λ0, ⋯, λℓ−1 are estimated so that the values predicted bythe model  are as close as possible to the figures actually observed
are as close as possible to the figures actually observed  . Specifically, we willl look for C, λ0, ⋯, λℓ−1 in the form
. Specifically, we willl look for C, λ0, ⋯, λℓ−1 in the form  and
and  with
with  and μ0, ⋯, μℓ−1 solutions to the constrained least squares minimizatio problem
and μ0, ⋯, μℓ−1 solutions to the constrained least squares minimizatio problem
 (A.12)
(A.12)
This problem can be written into the form
 (A.13)
(A.13)
where  contains all the unknow coefficients,
contains all the unknow coefficients,  is the rectangular matrix whose coefficients are
is the rectangular matrix whose coefficients are
![\[ (A)_{i, j} = {d^{\star}}_{L+1+i-m-j} \mbox{ for } 1 \leqslant i \leqslant K, \; 1 \leqslant j \leqslant \ell. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq69.png)
and  . This is a quadratic programming problem whose matrix is AtA which is positive semidefinite, but not generally positive definite. It will be replaced by the slightly perturbed problem
. This is a quadratic programming problem whose matrix is AtA which is positive semidefinite, but not generally positive definite. It will be replaced by the slightly perturbed problem
 (A.14)
(A.14)
where ε > 0 is a sufficiently small parameter and Iℓ is the identity matrix of size ℓ × ℓ (we will choose ε = 0.001 in practice). The matrix Qε is clearly defined positive and the problem (A.14) admits a unique solution  . Other constraints to this quadratic programming problem may be added, such as if we want to take into account the evolution of an infected person’s contagiousness. Indeed, contagiousness generally depends on the evolution of the viral load over the period of transmission. For example, it increases up to a maximum value and then decreases until the end of the contagiousness period. We choose to translate this into a constraint of the convexity type:
. Other constraints to this quadratic programming problem may be added, such as if we want to take into account the evolution of an infected person’s contagiousness. Indeed, contagiousness generally depends on the evolution of the viral load over the period of transmission. For example, it increases up to a maximum value and then decreases until the end of the contagiousness period. We choose to translate this into a constraint of the convexity type:
![\[ \mu_{i} \geqslant \frac{\mu_{i-1} + \mu_{i+1}}{2}, \mbox{ for } 1 \leqslant i \leqslant \ell-2, \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq74.png)
which we can rewrite as follows
 (A.16)
(A.16)
In addition, in order to avoid profiles with increasing coefficients, it is possible, for example, to indicate that the person is, on average, more contagious over the entire period than at the end, that is,
 (A.17)
(A.17)
Simple software was used to solve this optimization problem. Since the number of unknowns is very low in practice (ℓ = 17), the cost of the calculation is negligible. The values obtained for some countries are summarized in Table A.1.
Coefficients of coronavirus transmission Sars-2019 by country (calibrated) (FR: France, IT: Italy, ESP: Spain, USA: United States of America, UK: United Kingdom, GER: Germany, KOR: South Korea, BEL: Belgium, CHN: China, WR: World.
A.3 Coefficients of transmission by country (calibrated). Pandemic Covid-19
Some data sources:
-
Germany: Robert Koch Institut. SARS-CoV-2 in Germany
-
South Korea:Coronavirus information, South Korea
-
Spain: Rtve. Coronavirus España :
-
France: Santé Publique France Godes: geodes.santepubliquefrance.fr
Covid-19 en France: https://dashboard.covid19.data.gouv.fr/
-
Italy:Ministero della Salute: http://www.salute.gov.it.
-
United Kingdom: Coronavirus (COVID-19) cases in the UK:https://coronavirus.data.gov.uk/
-
USA: Johns Hopkins Coronavirus Resource Center: https://coronavirus.jhu.edu/map.html
CDC: https://www.cdc.gov/coronavirus/2019-ncov/cases-updates/cases-in-us.html
References
- H. Abbey, An examination of the Reed Frost theory of epidemics. Hum. Biol. 24 (1952) 201–233. [PubMed] [Google Scholar]
- R.M. Anderson and R.M. May, Infectious Diseases of Humans. Dynamics and Control. Oxford Univ. Press, Oxford (1992). [Google Scholar]
- R.M. Anderson, Discussion: The Kermack-McKendrick epidemic threshold theorem. Bull. Math. Biol. 53 (1991). [Google Scholar]
- J. Arino, F. Brauer, P. Van den Driessche, J. Watmough and J. Wu, Simple models for containment of a pandemic. J. Roy. Soc. Interface 3 (2006) 453–457. [CrossRef] [PubMed] [Google Scholar]
- J. Arino, F. Brauer, P. Van den Driessche, J. Watmough and J. Wu, A final size relation for epidemic models. Math. Biosci. Eng. 4 (2007) 159–176. [CrossRef] [PubMed] [Google Scholar]
- N.T.J. Bailey, The total size of a general stochastic epidemict. Biometrika 40 (1953) 177. [CrossRef] [Google Scholar]
- M.S. Bartlett, Stochastic Population Models in Ecology and Epidemiology. Methuen (1960). [Google Scholar]
- Q. Bi et al., Epidemiology and Transmission of COVID-19 in Shenzhen China: Analysis of 391 cases and 1,286 of their close contacts. The Lancet (2020). [Google Scholar]
- F. Brauer and C. Castillo-Chávez, Mathematical Models in Population Biology and Epidemiology. Springer, New York, Berlin, and Heidelberg (2001). [CrossRef] [Google Scholar]
- T. Britton and E. Pardoux (editors) Stochastic Epidemic Models with Inference. Vol. 2255 of Lecture Notes in Mathematics book series. Springer (2019). [CrossRef] [Google Scholar]
- D.J. Daley and J. Gani, Epidemic modelling. An introduction. Cambridge Studies in Mathematical Biology. Cambridge University Press, Cambridge (1999). [Google Scholar]
- G. De Natale et al., The Covid-19 Infection in Italy: a Statistical Study of an Abnormally Severe Disease J. Clin. Med. 9 (2020) 1564. [CrossRef] [Google Scholar]
- O. Diekmann and J.A.P. Heesterbeek, Mathematical Epidemiology of Infectious Diseases: Model building, Analysis and Interpretation. John Wiley & Sons (2000). [Google Scholar]
- Z. Du et al., Risk for transportation of 2019 novel coronavirus disease from Wuhan to other cities in China. Emerg. Infect. Dis. 26 (2020). [Google Scholar]
- S. Esposito and N. Principi, To mask or not to mask children to overcome COVID-19. Eur. J. Pediatr. 179 (2020) 1267–1270. [CrossRef] [Google Scholar]
- N. Ferguson et al., Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand, report 9, Imperial College COVID-19 Response Team (march 2020). [Google Scholar]
- S. Funk, M. Salathé and V.A.A. Jansenand, Modelling the influence of human behaviour on the spread of infectious diseases: a review. J. R. Soc. Interface 7 (2010) 1247–1256. [CrossRef] [PubMed] [Google Scholar]
- M. Greenwood, On the statistical measure of infectiousness. Hyg. Camb. 31 (1931) 336. [CrossRef] [Google Scholar]
- Q. Griette, P. Magal and O. Seydi, Unreported cases for age dependent COVID-19 outbreak in Japan. Biology 9 (2020) 132. [CrossRef] [Google Scholar]
- A.S. Gumel et al., Modeling strategies for controlling SARS outbreaks based on Toronto, Hong Kong, Singapore and Beijing experience. Proc. Roy. Soc. London 271 (2004) 2223–2232. [CrossRef] [Google Scholar]
- H.W. Hethcote, A thousand and one epidemic models. Frontiers in Mathematical Biology, edited by S.A. Levin. Vol. 100 of Lecture Notes in Biomathematics. Springer, Berlin, Heidelberg (1994). [Google Scholar]
- E. Hunter, B. Mac Namee and J.D. Kelleher, Using a socioeconomic segregation burn-in model to initialise an agent-based model for infectious diseases. J. Artific. Soc. Soc. Simul. 21 (2018) 9. [CrossRef] [Google Scholar]
- D. Juher, I.Z. Kiss and J. Saldaña, Analysis of an epidemic model with awareness decay on regular random networks. J. Theor. Biol. 365 (2015) 457–468. [CrossRef] [PubMed] [Google Scholar]
- W. Just, J. Saldaña and Y. Xin, Oscillations in epidemic models with spread of awareness. J. Math. Biol. 76 (2018) 1027–1057. [CrossRef] [PubMed] [Google Scholar]
- W.O. Kermack and A.G. McKendrick, A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. Lond. A 115 (1927) 700–21. [CrossRef] [Google Scholar]
- W.O. Kermack and A.G. McKendrick, Contributions to the mathematical theory of epidemics. Part II. Proc. Roy. Soc. London 138 (1932) 55–83. [Google Scholar]
- S.A. Lauer et al., The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 10 (2020). [Google Scholar]
- F.-X. Lescure et al., Clinical and virological data of the first cases of COVID-19 in Europe: a case series. The lancet (2020). [Google Scholar]
- N. Linton et al., Incubation period and other epidemiological characteristicsof 2019 novel coronavirus infections with right truncation: a statisticalanalysis of publicly available case data. J. Clin. Med. 9 (2020) 538. [CrossRef] [Google Scholar]
- N.M. Linton, T. Kobayashi, Y. Yang et al., Epidemiological characteristics of novel coronavirus infection: a statistical analysis of publicly available case data. J. Clin. Med. 9 (2020) 538. [CrossRef] [Google Scholar]
- Z. Liu, P.Magal, O. Seydi and G. Webb, Understanding unreported cases in the COVID-19 epidemic outbreak in wuhan, china, and the importance of major public health interventions. Biology 9 (2020) 50. [CrossRef] [Google Scholar]
- Z. Liu, P.Magal, O. Seydi and G. Webb, A COVID-19 epidemic model with latency period. Infect. Disease Model. 5 (2020) 323–37. [CrossRef] [Google Scholar]
- Q. Li, X. Guan, P. Wu et al., Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 382 (2020) 1199–1207. [Google Scholar]
- Y. Ohkusa and T. Sugawara, Application of an individual-based model with real data for transportation mode and location to pandemic influenza. J. Infect. Chemother. 13 (2007) 380–9. [CrossRef] [Google Scholar]
- A. Perasso, An introduction to the basic reproduction number in mathematical epidemiology. ESAIM: PS 62 (2018) 123–138. [Google Scholar]
- G. Rinaldi and M. Paradisi, An empirical estimate of the infection fatality rate of COVID-19 from the first Italian outbreak. Preprint medRxiv DOI: 10.1101/2020.04.18.20070912 (2020). [Google Scholar]
- T.W. Russell et al., Estimating the infection and case fatality ratio for coronavirus disease (COVID-19) using age-adjusted data from the outbreak on the Diamond Princess cruise ship. Euro Surveill. 26 (2020) 2000256. [Google Scholar]
- H. Salje, C. Tran Kiem, N. Lefrancq, N. Courtejoie, P. Bosetti et al., Estimating the burden of SARS-CoV-2 in France, https://hal-pasteur.archives-ouvertes.fr/pasteur-02548181 HAL, (2020). [Google Scholar]
- A. Perasso, An introduction to the basic reproduction number in mathematical epidemiology. ESAIM: PS 62 (2018) 123–138. [Google Scholar]
- F.D. Sahneh, F.N. Chowdhury and C.M. Scoglio, On the existence of a threshold for preventive behavioral responses to suppress epidemic spreading. Sci. Rep. 2 (2012) 632. [CrossRef] [PubMed] [Google Scholar]
- X. Tang et al., On the origin and continuing evolution of SARS-CoV-2. National Sci. Rev. 7 (2020) 1012–23. [CrossRef] [Google Scholar]
- H.R. Thieme, Mathematics in Population Biology. Princeton Univ. Press, Princeton and Oxford (2003). [Google Scholar]
- R. Verity, Estimates of the severity of coronavirus disease 2019: a model-based analysis. The Lancet 20 (2020) 669–677. [CrossRef] [Google Scholar]
- L. Willem, F. Verelst, J. Bilcke, N. Hens and P. Beutels Lessons from a decade of individual-based models for infectious disease transmission: a systematic review (2006–2015). Infect. Diseases 17 (2017) 612. [Google Scholar]
- E. Williamson et al., OpenSAFELY: factors associated with COVID-19-related hospital death in the linked electronic health records of 17 million adult NHS patients. Preprint medRxiv (2020). doi:10.1101/2020.05.06.20092999. [Google Scholar]
- P. Whittle, The outcome of a stochastic epidemic – a note on Baily’s paper. Biometrika 42 (1955) 116–122. [Google Scholar]
- J.T. Wu, K. Leung, et al., Estimating clinical severity of covid-19 from the transmission dynamics in Wuhan, China. Nat. Med. 26 (2020) 506–10. [CrossRef] [PubMed] [Google Scholar]
- P. Yubero, A.A. Lavin and J.F. Poyatos, Evidence for immunity to SARS-CoV-2 from epidemiological data series. Preprint MedRxiv (2020) doi:2020.07.22.20160028. [Google Scholar]
- S. Zhao, D. Gao, Z. Zhuang, M. Chong et al., Estimating the serial interval of the novel coronavirus disease (COVID-19): a statistical analysis using the public data in Hong Kong. To appear in: Front. Phys. (2020) https://doi.org/10.3389/fphy.2020.00347. [Google Scholar]
- J. Zhang et al., Evolving epidemiology and transmission dynamics of coronavirusdisease 2019 outside Hubei province, China: a descriptive and modelling study. The Lancet 20 (2020) 793–802. [Google Scholar]
- F. Zhou et al., Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. The Lancet 395 (2020) 1054–1062. [CrossRef] [PubMed] [Google Scholar]
- N. Zhu et al., A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 382 (2020) 727–733. [Google Scholar]
- L. Zou, F. Ruan et al., SARS-CoV-2 Viral Load in Upper Respiratory Specimens of Infected Patients. N. Engl. J. Med. 382 (2020) 12. [CrossRef] [Google Scholar]
This fact may seem surprising, but the explanation is simple. Let us recall that in the model (2.3), the number of deaths is calculated from the deaths already recorded. It is not necessary to go through the number of infected individuals (which is generally imprecise or even unknown). On the other hand, estimating the number of infected cases will require setting a fatality rate per infection.
All Tables
Scenario 0 (evolution of the epidemic in France without strict lockdown on March 17th 2020). Main indicators on the date of relaxing lockdown (May 11th), June 15th, July 31st and August 31st 2020.
Scenario 1 (continuation of lockdown in France after May 11th 2020). Main indicators at the date of relaxing lockdown (11/5/2020), June 15th, July 31st and August 31st 2020.
Coefficients of coronavirus transmission Sars-2019 by country (calibrated) (FR: France, IT: Italy, ESP: Spain, USA: United States of America, UK: United Kingdom, GER: Germany, KOR: South Korea, BEL: Belgium, CHN: China, WR: World.
All Figures
 |
Fig. 1 The ratio γn calculated from March 31st to April 24th 2020. It can be observed that this ratio is almost constant, confirming the assumed proportionality of the two quantities. |
| In the text | |
 |
Fig. 2 Evolution of the daily reproduction number for China for the period from January 23rd to March 3rd 2020 during the Coronavirus Sars-CoV-2 pandemic. This number is calculated from mortality data. |
| In the text | |
 |
Fig. 3 Evolution of the daily reproduction number for France, Italy and Spain for the period from February 23rd to April 6th 2020 during the Coronavirus Sars-CoV-2 pandemic. This number is calculated from mortality data. |
| In the text | |
 |
Fig. 4 Evolution of the daily reproduction number for Belgium, Germany and South Korea from February 28th to April 5th 2020 (Covid-19 pandemic). |
| In the text | |
 |
Fig. 5 Evolution of the daily reproduction number for the period from the end of February to the beginning of April 2020 for the United States and the United Kingdom (Covid-19 pandemic). |
| In the text | |
 |
Fig. 6 Scenario 0 in France. Left: total number of deaths in hospital. Right: daily deaths in hospital. Values up to March 17th 2020 are actual (public data). |
| In the text | |
 |
Fig. 7 Scenario 0 in France. Left: number of occupied ICU beds (estimated by the model). Right: evolution of the number of active cases, the number of infected individuals and the number of recoveries until early December 2020 (estimated by the model). We observe that the peak of the epidemic occurs at the beginning or end of June 2020, depending on the value of the IFR. Values up to March 17th 2020 are actual (public data). |
| In the text | |
 |
Fig. 8 Scenario 1 in France. Left: total number of deaths in hospital. Right: daily deaths in hospital. Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 9 Scenario 1 in France. Left: number of occupied ICU beds (estimated by the model). Right: number of active cases, of the number of infected persons and of recovered persons until December 4th 2020 (estimated by the model). Values up to April 30th 2020 are real (public data). |
| In the text | |
 |
Fig. 10 Deconfinement Scenarios 2 and 3 (France). Left: total number of deaths in hospital. Right: daily deaths in hospital. Scenario 1 of continuation of strict lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 11 Deconfinement Scenarios 2 and 3 (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 12 Deconfinement Scenarios 2 and 3 (France). Total number of infected individuals until early March 2021. |
| In the text | |
 |
Fig. 13 Scenarios 4 and 5 of periodic deconfinement (France). Left: total number of deaths in hospital. Right: daily deaths in hospital. Scenario 1 of continuation of strict lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 14 Scenarios 4 and 5 of periodic deconfinement (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 15 Scenarios 4 and 5 of periodic deconfinement (France). Total number of infected individuals until early March 2021. |
| In the text | |
 |
Fig. 16 Scenarios 6 to 10: weekly organized deconfinement (France). Left: total (cumulative) number of deaths in hospital. Right: deaths in hospital. Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 17 Scenarios 6 to 10: weekly organized deconfinement (France). Left: number of occupied ICU beds (estimated by the model). Right: number of active cases until March 4th 2021 (estimated by the model). Scenario 1 of continuation of lockdown is shown for comparison. All Values up to April 30th 2020 are actual (public data). |
| In the text | |
 |
Fig. 18 Scenarios 6 to 10: weekly organized deconfinement (France). Total number of infected individuals until early March 2021. |
| In the text | |
 |
Fig. 19 Simplified four-lanes diagram showing the levels of interventions to curb the epidemic. |
| In the text | |
 |
Fig. 20 Superposition of the limits of the four lanes with the evolution of the daily reproduction number for France, Italy and Spain (for the period from February 23rd to April 2nd 2020 during the Coronavirus Sars-Cov-2 pandemic) |
| In the text | |
 |
Fig. 21 Simplified diagram of a zigzag strategy by a weekly organized deconfinement. Here we have chosen Monday and Thursday as days of deconfinement. The other days of the week are lockdown days. Schematically, deconfinement amounts to a changeof lane, which can go up to the intermediate lane (because only two days per week are deconfined). The relaxed lane is excluded (or forbidden). When the number of days of deconfinement increases, the intermediate lane may become excluded as well. |
| In the text | |
 |
Fig. 22 Simplified diagram of a zigzag strategy by periodic deconfinement. Strict lockdown and moderate deconfinement alternate over equal periods of time. Schematically, deconfinement amounts to a change of lane. The intermediate lane and the relaxed lane are prohibited in this strategy. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.












![\[ D_n \ll \alpha P. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq54.png)
![\[ A^{\star}_n = \sum_{k=0}^{n} (a_n -a_{n-p}) = A_n - A_{n-p}. \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq58.png)
![\[ A^{\star}_n = \frac{\beta}{\alpha} (D_{n+r-t} - D_{n+r-(t+p)}) \]](/articles/mmnp/full_html/2020/01/mmnp200131/mmnp200131-eq59.png)
